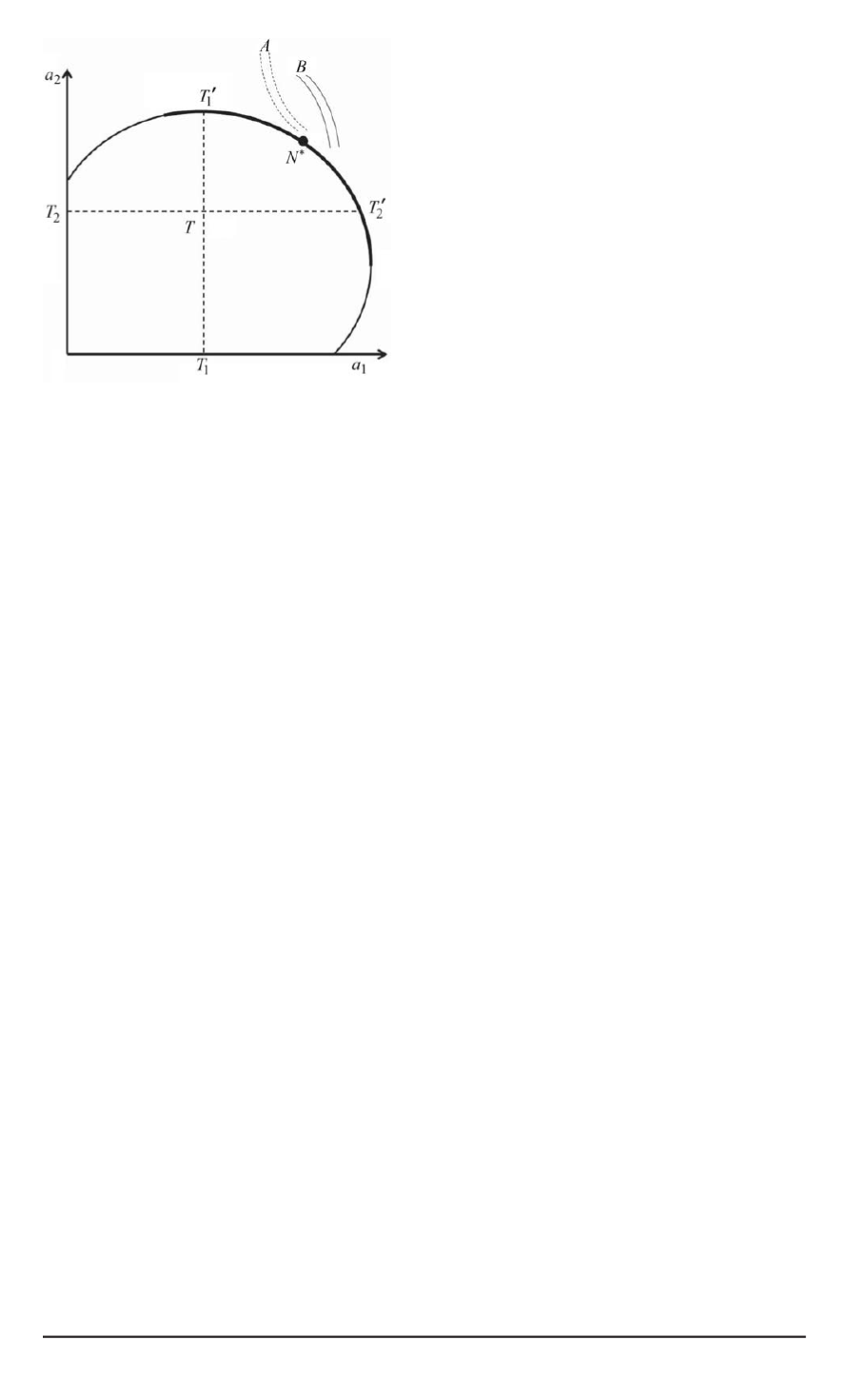
Рис. 2. Исходы кооперативной игры
[13]
стратегий в одиночку, т.е. выигры-
ши
a
1
и
a
2
игроков удовлетворяют
условиям [13]
a
1
(
x, y
opt
)
a
1
(
х
opt
, y
opt
)
,
a
2
(
х
opt
, y
)
a
2
(
х
opt
, y
opt
)
(4)
для любых стратегий
х
и
y
. В теории
игр доказано, что для любой конеч-
ной некооперативной игры с ненуле-
вой суммой существует по крайней
мере одна равновесная пара сме-
шанных стратегий. В общем слу-
чае равновесие может бытьне един-
ственным, причем каждому из них
могут соответствоватьразные значения выигрышей у игроков.
В случае кооперативной игры с двумя игроками предполагается,
что игроки не могут воздействоватьдруг на друга до тех пор, пока не
придут к некоторому соглашению. Тогда исходы игры представимы
на плоскости общих выигрышей
a
1
и
a
2
в виде множества
S
(рис. 2),
где
T
1
и
T
2
— значения выигрышей, которые могут получитьсоответ-
ственно игроки 1 и 2 без кооперации с партнером. В предположении
о том, что множество
S
является выпуклым, замкнутым и ограни-
ченным сверху, оптимальные решения находятся на правой верхней
его границе. На ней выделяется участок
T
1
T
2
— множество Парето-
оптимальных решений
˜
N
, на котором увеличение выигрыша одного
игрока возможно только за счет уменьшения выигрыша его партнера;
оно называется переговорным множеством. Игрокам не имеет смысла
вести переговоры относительно решений вне множества
˜
N
, посколь ку
положение одного из них может бытьлибо улучшено без ущерба для
партнера, либо он может достичьлучшего выигрыша в одиночку.
На переговорном множестве
˜
N
выделяется точка
N
∗
, соответству-
ющая равновесию по Нэшу. В ней достигаетcя максимум произведе-
ния
max[(
a
1
−
T
1
)(
a
2
−
T
2
)] = [
a
1
−
T
1
(
N
∗
)][
a
2
−
(
T
2
(
N
∗
)]
,
(5)
в котором сомножители представляют собой превышения выигрышей
каждого из игроков над платежами, которые могут бытьполучены
игроками без кооперации. Равновесие по Нэшу соответствует компро-
миссному оптимуму стратегий обоих игроков.
Отметим здесьаналогию с классическим портфельным анализом,
когда инвестору приходится выбиратьразумный компромисс между
величиной ожидаемой доходности портфеля и его риском. Склонность
80
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 1


