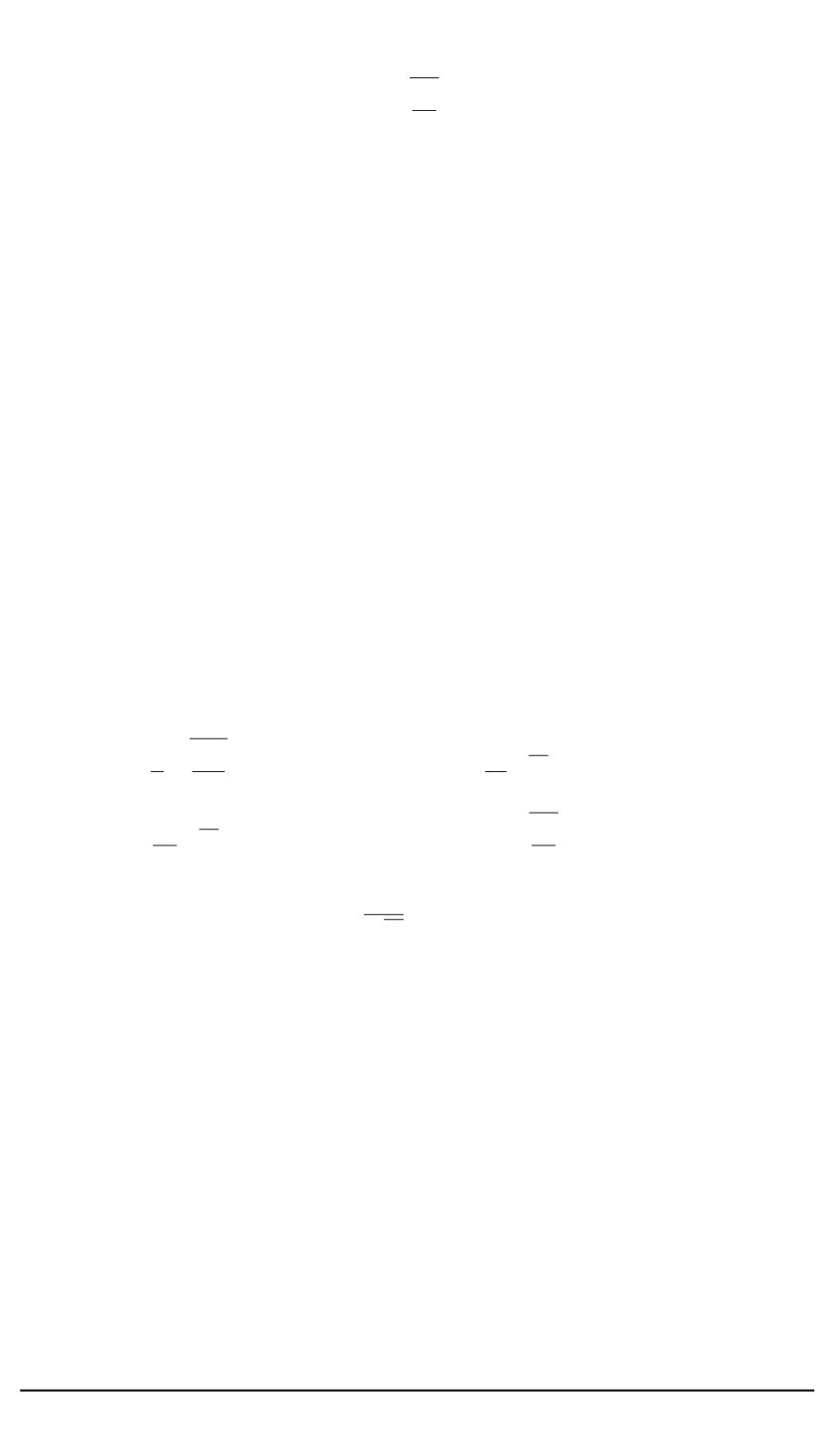
энергию, которая, естественно, соответствует планковской массе
m
0
:
E
0
=
m
0
c
2
=
c
2
c
G
= 1
,
2
·
10
19
ГэВ
.
Планковская длина и планковская энергия лежат столь далеко за преде-
лами экспериментальныхвозможностей, что, быть может, человечество не
сможет достичь ихна протяжении не только ближайшихстолетий, но и на
протяжении всего своего существования. Эти величины чрезвычайно удоб-
ны для теоретиков в том смысле, что они дают возможность на протяжении
всей своей жизни не опасаться ни экспериментального подтверждения, ни
опровержения теоретическихрезультатов.
Однако, возможно, дело обстоит несколько иначе. В работе автора [2]
построена расширенная система планковскихвеличин с включением в нее
кроме гравитационной постоянной, скорости света и постоянной Планка
еще и элементарного заряда. В этой системе планковские длина, время
и масса умножаются еще на безразмерную постоянную тонкой структуры
α
=
e
2
/ c
в произвольной степени. Такая система становится бесконечно-
значной. Расширяя эту конструкцию [3], показатель степени можно взять
в виде комплексной и даже гиперкомплексной величины, и, таким образом,
число измерений пространства увеличивается, оно становится комплексным,
гиперкомплексным, многомерным.
В бесконечнозначной расширенной системе планковскихвеличин есть
величины, в определенном смысле, выделенные. Это те величины, в которых
отсутствует та или иная из четырехфундаментальныхмировыхконстант [2].
Приведем эти величины (нас здесь интересуют длина и энергия):
l
0
=
1
c
G
c
= 1
,
61
·
10
−
33
см
;
l
1
=
e
c
2
√
G
= 1
,
37
·
10
−
34
см
;
l
2
=
2
e
3
√
G
= 2
,
62
·
10
−
30
см
;
E
0
=
c
2
c
G
= 1
,
2
·
10
19
ГэВ
;
E
1
=
c
2
e
√
G
= 10
18
ГэВ
.
Существуют ли в этой бесконечнозначной расширенной системе план-
ковскихвеличин выделенные по каким-то другим принципам величины —
этот вопрос на сегодня остается открытым.
На основе полученныхавтором результатов в вопрос о компактифика-
ции дополнительныхизмерений можно ввести определенные дополнения и
модификации. Нам кажется, что в этом направлении возможны три варианта.
1. Компактификация дополнительныхизмерений отсутствует, а сами эти
дополнительные измерения почти не проявляются в обычном трехмерном
пространстве, так как они имеют мнимый характер и дуальны обычным
измерениям.
2. Масштабы компактификации дополнительныхизмерений могут быть
по каким-то критериям выбраны из совокупности бесконечнозначной рас-
ширенной системы планковскихвеличин.
3. Масштабы пространственной ячейки, связанной с компактификацией
дополнительныхизмерений или с квантованием пространства-времени не
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 3
127