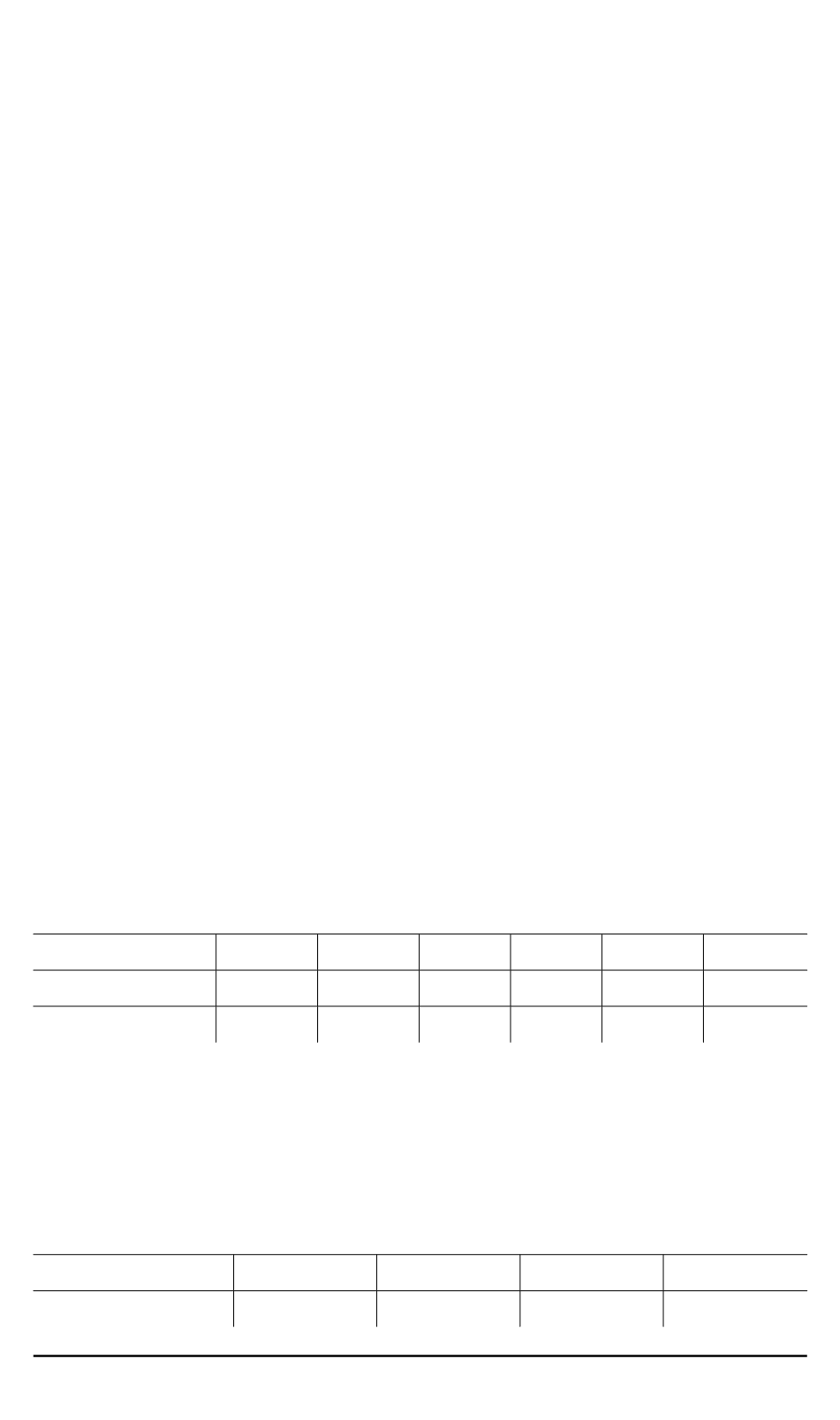
Дальнейшее увеличение размерности системы приводит к тому, что
размер хранимых данных превышает объем доступной оперативной
памяти (суммарно 96 Гбайт на все вычислительные модули) и часть
данных сохраняется в виртуальной памяти на жестком диске, что в
несколько раз снижает производительность системы в целом. Пред-
ставленный пример убедительно доказывает, что для оценки произво-
дительности кластера в дальнейшем достаточно проводить расчеты с
матрицами наибольшего доступного размера.
Приведенные данные относятся к расчетам, в которых кластер-
ная система конфигурировалась как смешанная MPP-машина с восе-
мью SMP-модулями. Подобный подход, использующий технологию
OpenMP для систем с общей памятью, по-видимому, позволяет опти-
мально использовать вычислительные ресурсы, сосредоточенные на
одном узле кластера.
В табл. 2 приведена производительность системы для случая, когда
кластер конфигурировался как “чистая” MPP-машина из 32 вычисли-
тельных модулей. Хотя на оценку производительности существенно
влияет способ распределения блоков матрицы между вычислительны-
ми модулями (числа
P
и
Q
), во всех вариантах наблюдается значитель-
ное снижение производительности, что связано с возрастанием числа
и сложности организации обменов между вычислительными модуля-
ми. Кроме того, такая логическая структура кластера приводит к до-
полнительным затратам оперативной памяти на хранение служебной
информации, поэтому максимальный размер обрабатываемой матри-
цы становится несколько меньше. В табл. 2 приведены данные для
N
= 90 000
в сравнении с соответствующим результатом из табл. 1.
Таблица 2
Производительность структуры из 32 MPP-модулей
P
×
Q
1
×
32 2
×
16 4
×
8 8
×
4 16
×
2 32
×
1
R
32
, Гфлопс
187,7 200,9 198,0 174,6 121,8
68,1
R
32
/R
8
∙
100 %
78,4
83,9
82,7
72,9
50,9
28,4
Зависимость производительности кластера от соотношения
P
×
Q
проявляется и для случая восьмимодульного кластера с SMP-машина-
ми. В табл. 3 приведены результаты расчетов для
N
= 110 000
.
Таблица 3
Производительность структуры из 8 SMP-модулей
P
×
Q
1
×
8
2
×
4
4
×
2
8
×
1
R
8
, Гфлопс
240,3
258,7
250,5
210,6
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 4
37


