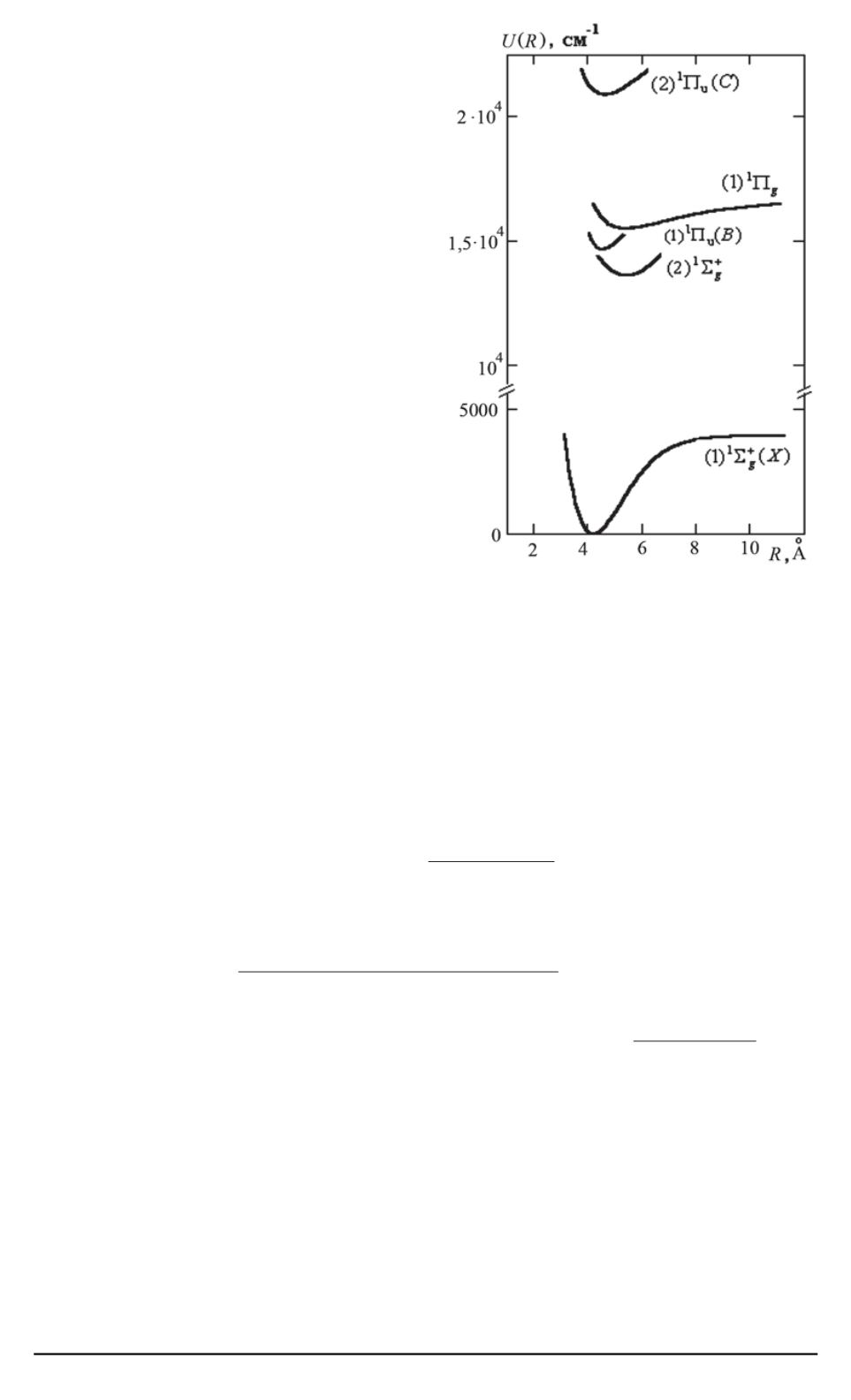
Рис. 1. Экспериментально изученные
участки потенциальных кривых для
основного и возбужденных электрон-
ных состояний димерарубидия
Параметры функций ВМ и
поворотные точки потенциальных
кривых РКР рассчитаны по про-
граммам [3, 13] с использова-
нием экспериментальных колеба-
тельных и вращательных постоян-
ных для возбужденных состояний
85
Rb
2
[14–18]. Параметры функции
(6) получены методом наимень-
ших квадратов с помощью пово-
ротных точек
R
max
потенциальных
кривых РКР и экспериментальных
значений энергий диссоциации.
В табл. 1 приведены рассчитан-
ные поворотные точки потенциа-
лов РКР для возбужденных состо-
яний, а на рис. 1 — построенные
в настоящей работе эксперимен-
тально изученные участки потен-
циальных кривых возбужденных
и основного электронных состоя-
ний молекулы Rb
2
. Вращательные
и центробежные постоянные рассчитаны по теории возмущений для
модели вращающегося осциллятора двухатомной молекулы [19]:
B
v
=
β v
|
R
−
2
|
v
;
(7)
D
v
=
β
2
u
=
v
u
|
R
−
2
|
v
2
(
E
u
−
E
v,
)
;
(8)
H
v
=
β
3
t
=
v u
=
v
v
|
R
−
2
|
u u
|
R
−
2
|
t t
|
R
−
2
|
v
(
E
u
−
E
v
)(
E
t
−
E
v
)
−
−
β
2
B
v
u
=
v
u
|
R
−
2
|
v
2
(
E
u
−
E
v
)
2
,
(9)
где матричный элемент
u
|
R
−
2
|
v
=
∞
0
ψ
u
(
R
)
R
−
2
ψ
v
(
R
)
dR.
Необходимые для расчета колебательные энергии и волновые функ-
ции найдены в результате численного решения радиального волнового
уравнения на основе построенных потенциальных кривых.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 4
63


