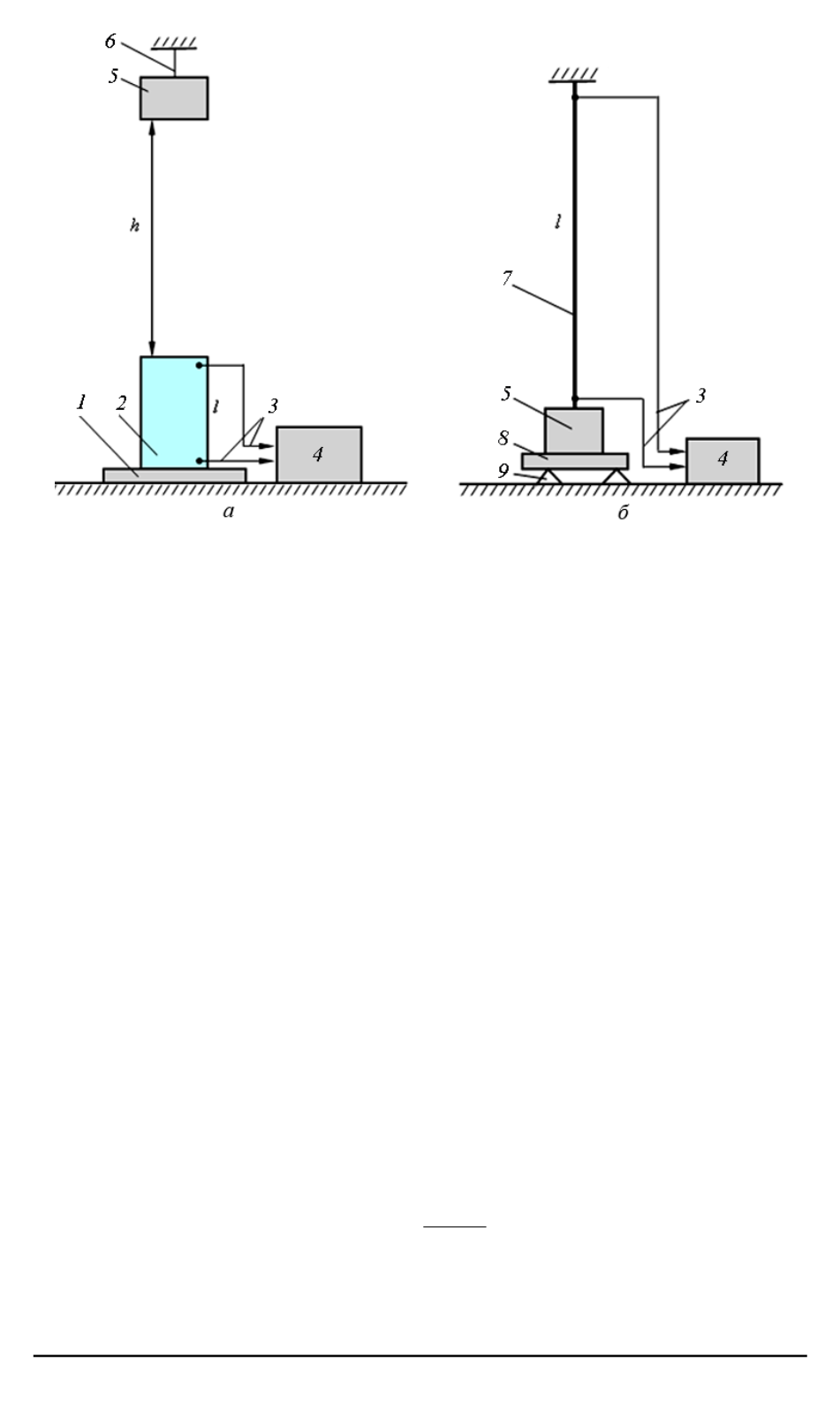
Рис. 1. Схема проведения опыта с деформированными телами:
а
— деформация сжатия при ударе;
б
— деформация растяжения при статической
нагрузке;
1
— диэлектрическая плита;
2
— испытуемый образец (параллелепипед);
3
— токоподвод к гальванометру;
4
— баллистический гальванометр;
5
— груз;
6
— нить подвеса;
7
— испытуемый образец (проволока);
8
— диэлектрическая
платформа;
9
— опоры
же образом производился удар, но с последующей постоянной нагруз-
кой на образец. Соответственно, деформация сжатия имела место при
снятии нагрузки.
Во всех наблюдаемых опытах при ударной нагрузке медный ци-
линдр отскакивал от образца, что позволило при интерпретации
результатов с некоторым приближением считать удар упругим. Во
всех случаях фиксировался прошедший через гальванометр заряд
(0
,
7
. . .
1)
∙
10
−
6
Кл. К сожалению, этот результат не позволяет с
приемлемой точностью определить силу электрического тока, про-
текающего через образец, поскольку неизвестна продолжительность
этого процесса
τ
. Вычисления, проведенные с использованием закона
сохранения энергии
mgh
=
k
(Δ
l
)
2
/
2
, где
k
— коэффициент жесткости
образца,
Δ
l
— величина деформации, и закона Гука
σ
=
<
ε
(
σ
=
F/S
— нормальное напряжение,
F
— продольная сила,
S
— площадь попе-
речного сечения образца,
<
— модуль Юнга,
ε
= Δ
l/l
— относительное
удлинение), позволили оценить величину деформации
Δ
l
=
p
2
w/
<
l.
(1)
Здесь
w
— объемная плотность механической энергии в образце при
ударе (
w
=
W/V, W
=
mgh
). При этом
k
=
<
S/l
. Записывая далее
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1
41


