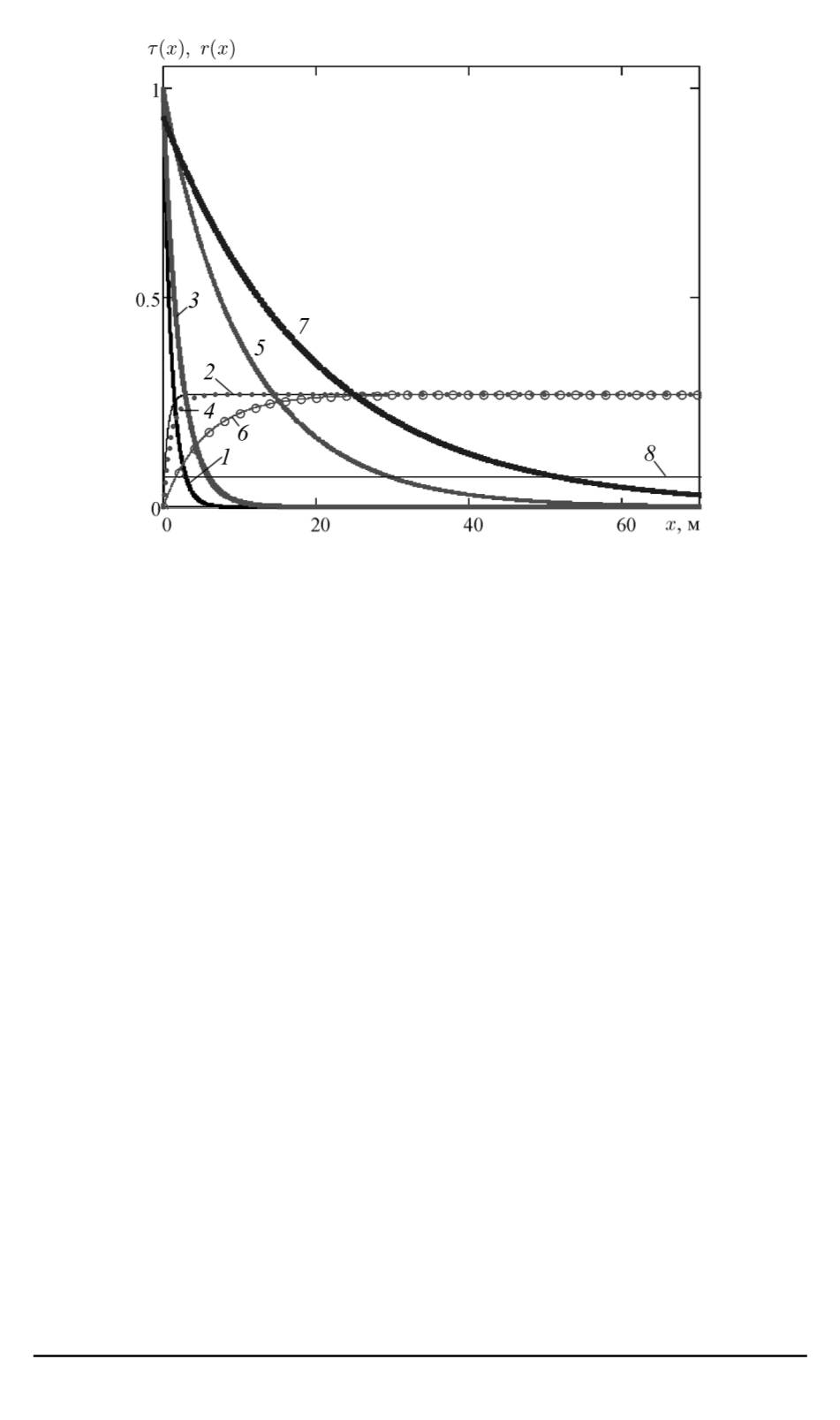
Рис. 2. Зависимость коэффициентов пропускания
τ
(
x
)
и отражения
r
(
x
)
от
толщины
x
подповерхностного слоя океана для оптических моделей (см.
таблицу):
1, 2
—
M
2(0
,
5
/
0
,
5
−
27)
;
3, 4
—
M
3(0
,
25
/
0
,
25
−
27)
;
5, 6
—
M
4(0
,
05
/
0
,
05
−
27)
;
7,
8
—
MCW
способность границы раздела двух сред определяется постоянной ве-
личиной 8. . . 10%, в которой не более 2–5% (в зависимости от угла
падения) соответствует френелевскому отражению, а остаток — отра-
жению от вспененной поверхности океана. Это поверхностное отра-
жение не зависит от толщины слоя вещества (кривая
8
). Если в такой
воде имеется рассеивающая примесь с показателем рассеяния, равным
показателю поглощения,
κ
4
=
σ
4
≈
κ
CW
= 0
,
05
м
−
1
, то отражение уже
является функцией толщины, возрастает до
0
,
27
на глубине
0
,
2
м
(так называемая толщина полубесконечного слоя) и с ростом толщи-
ны больше не изменяется. Для других вариантов рассеивающих слоев
ВНЭ за счет подбора показателей поглощения и рассеяния удается
изменить поглощение в слое морской воды, но альбедо толстого по-
лубесконечного слоя в данных расчетах одинаковое, характерное для
загрязненного океана.
На рис. 3 приведены расчетные распределения температуры по глу-
бине, формируемые в толще морской воды на третьи сутки (
tday
= 24
ч)
в астрономические полдень
t
= 2
,
25
∙
tday
и полночь
t
= 2
,
75
∙
tday
при синфазных колебаниях температуры атмосферы от
17
до
27
◦
С и
потока солнечного излучения от 500 Вт/м
2
до 0. Проведены расчетные
оценки температурных распределений в толще океана, загрязненного
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1
115


