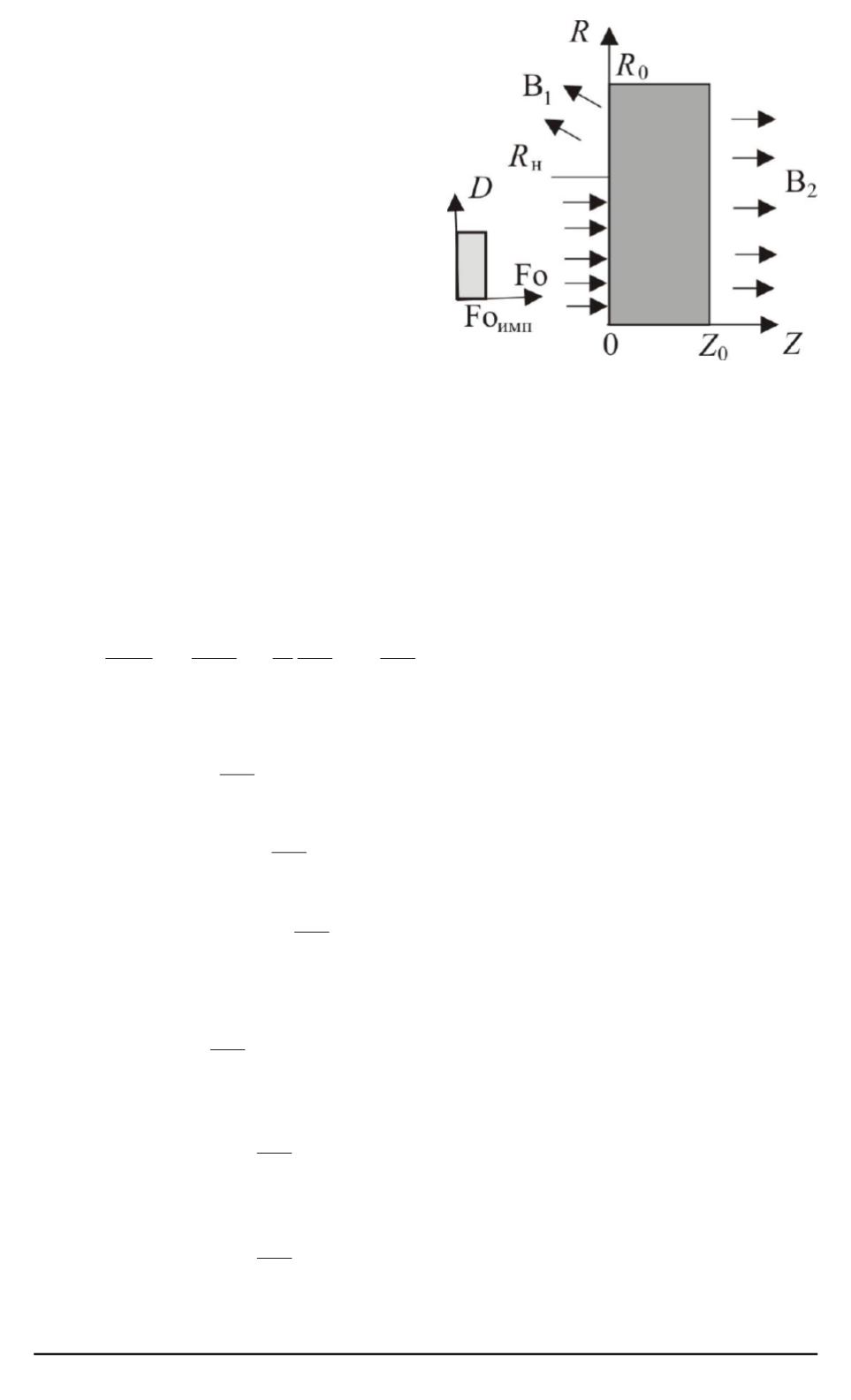
Рис. 1. Схемаобласти решения
Приняты следующие обозначе-
ния:
r, z
— текущие координаты;
r
н
— радиус лазерного луча;
ε
— при-
веденная степень черноты поверх-
ности материала;
σ
— постоянная
Стефана–Больцмана;
T
0
,
T
,
T
e
—
начальная, текущая температуры и
температура окружающей среды.
Задача решалась при использо-
вании безразмерных переменных в
осесимметричной постановке. Па-
раметрам
z, r, z
0
, r
0
, r
н
, T
0
, T, T
e
со-
ответствуют их безразмерные (см.
рис. 1) аналоги
Z
=
z/z
0
;
R
=
r/z
0
;
Z
0
= 1
;
R
0
=
r
0
/z
0
;
R
н
=
r
н
/z
0
;
θ
=
T/T
e
;
θ
0
=
T
0
/T
e
. При этом введены безразмерные критерии [7, 8]
D
=
qz
0
/λT
e
;
B
=
εσT
3
e
z
0
/λ
; Fo
=
at/z
2
0
, где Fo — критерий Фурье;
t
— время.
Задача сводится к решению нестационарного уравнения теплопро-
водности с соответствующими граничными и начальным условиями:
∂T
∂
Fo
=
∂
2
T
∂Z
2
+
1
R
∂
∂R
R
∂θ
∂R
,
0
< R < R
0
,
0
< Z <
1;
(1)
при
Z
= 0
−
∂θ
∂Z
=
D
+
B
1
θ, R R
н
,
Fo Fo
имп
;
(2)
−
∂θ
∂Z
=
B
1
θ, R > R
н
,
Fo
>
0;
(3)
−
∂θ
∂Z
=
B
1
θ,
Fo
>
Fo
имп
;
(4)
при
Z
=
Z
0
−
∂θ
∂Z
=
B
2
θ,
0
< R < R
0
,
Fo
>
Fo
имп
;
(5)
при
R
= 0
∂θ
∂R
= 0
,
0
< Z <
1
,
Fo
>
0;
(6)
при
R
=
R
0
∂θ
∂R
= 0
,
0
< Z <
1
,
Fo
>
0
.
(7)
При Fo
= 0
θ
= 1
.
(8)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 4
101


