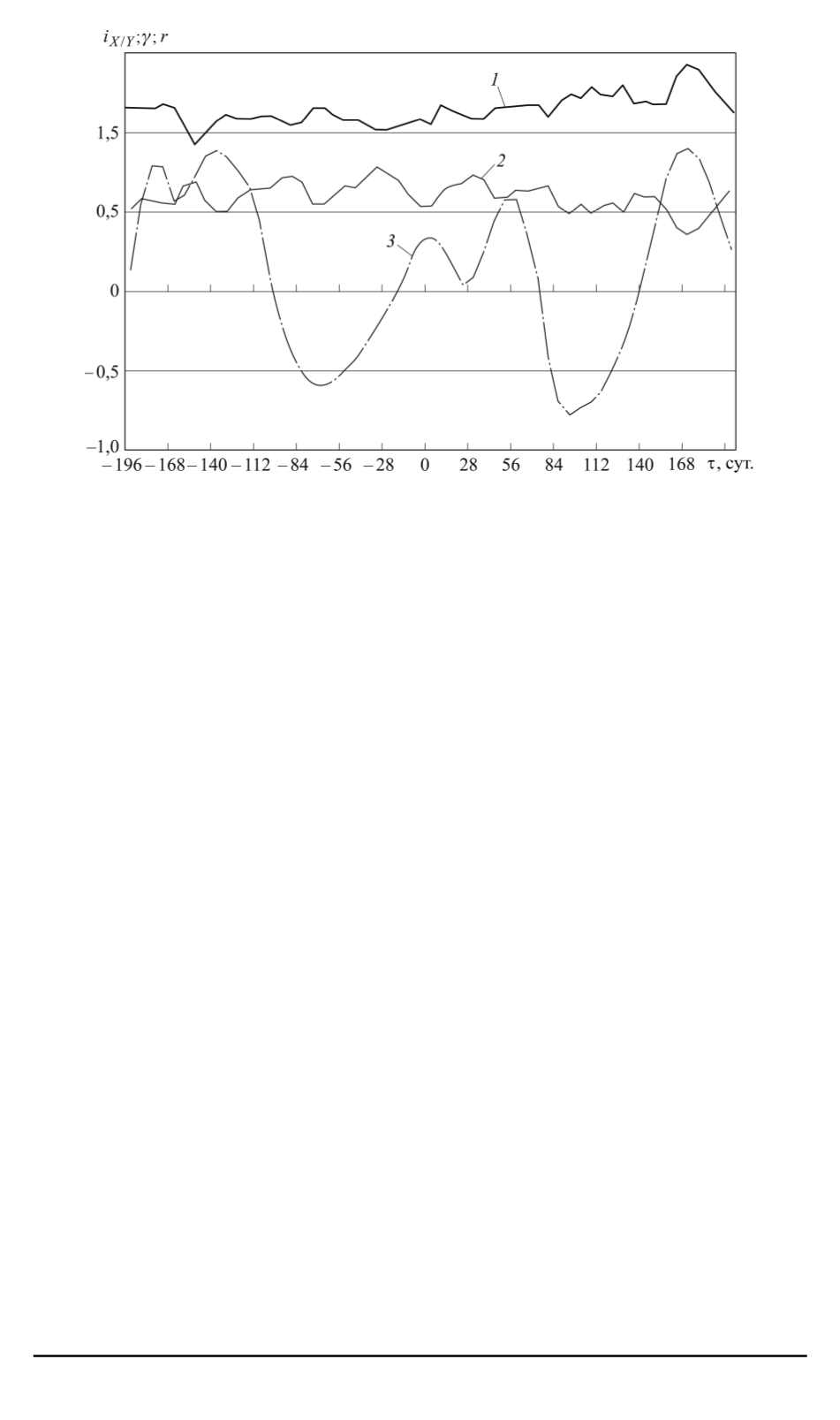
Рис. 8. Результаты причинного и корреляционного анализа данных
γ
(
1
),
i
X
|
Y
(
2
) и
r
(
3
) с детектора
U
t
(
X
)
и
XR
(
Y
)
при
τ
<
0
соответствуют
запаздыванию данных с детектора
U
t
относительно активности
XR
, при
τ
>
0
— опережению
анализа представлен на рис. 8. Главный максимум
γ
= 1
,
4
и глав-
ный минимум
i
X
|
Y
= 0
,
36
наблюдаются при опережении 168 сут. Им
соответствует максимум корреляции
r
≈
0
,
90
. Симметричный по вре-
мени
τ
запаздывающий экстремум слабее, он хорошо заметен только
у корреляции
r
и почти подавлен в функции
γ
. Столь большое время
опережения характерно для процессов большого пространственного
масштаба, каким является солнечная активность [18, 19, 29].
В приложении к прогнозу случайной компоненты солнечной ак-
тивности наиболее эффективен ранее разработанный и успешно при-
менявшийся алгоритм, основанный на расчете текущей импульсной
переходной характеристики, которая оптимально учитывает сложный
характер корреляционной функции [18, 23, 28, 29]. Однако его при-
менение возможно, если длина наблюдений многократно превышает
опережение прогноза. В данном случае для демонстрации возможно-
сти прогноза, как и в случае прогноза скорости
V
, будем использовать
алгоритм простой скользящей регрессии. Результат представлен на
рис. 9. Подобно прогнозу скорости
V
, он получен путем ежедневного
прогностического расчета активности
XR
с фиксированным опереже-
нием 168 сут. Показанная серия демонстрирует достаточную эффек-
тивность прогнозов — их среднеквадратическая погрешность в 6 раз
меньше размаха изменений активности
XR
. Отметим, что прогноз
на основе нелокальных корреляций касается именно случайной (не
детерминированной эволюцией) компоненты прогнозируемой величи-
ны. В этом его принципиальное отличие от прочих методов прогнозов,
46
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 1


