Следует отметить удовлетворительное согласие расчетных и экс-
периментальных данных, в связи с чем трудно отдать предпочтение
какому-либо варианту расчета. Распределение давления на стенке за
уступом характеризуется ярко выраженным максимумом вблизи ко-
ординаты
x/h
S
= 5
. . .
6
, причем уровень давления здесь несколь-
ко превышает первоначальный, который был на стенке перед отры-
вом. Протяженность почти изобарической донной области с низким
уровнем давления соответствует примерно 1,5. . . 2,0 высотам уступа,
а наибольший градиент давления на стенке в направлении течения
наблюдается именно в окрестности точки присоединения РЛТ.
Эксперименты и расчет показали, что теплоподвод за уступом в
рассматриваемых условиях и в исследованном диапазоне
q
c
≤
10
кВт/м
2
не оказывает заметного влияния на распределение давления на стенке,
а значит и на все поле течения.
Минимальные расчетные касательные напряжения на стенке за
уступом наблюдаются в окрестности точки
R
присоединения РЛТ, а
положение экстремально высоких значений этого параметра хорошо
коррелирует с координатой наибольшего значения давления на стенке
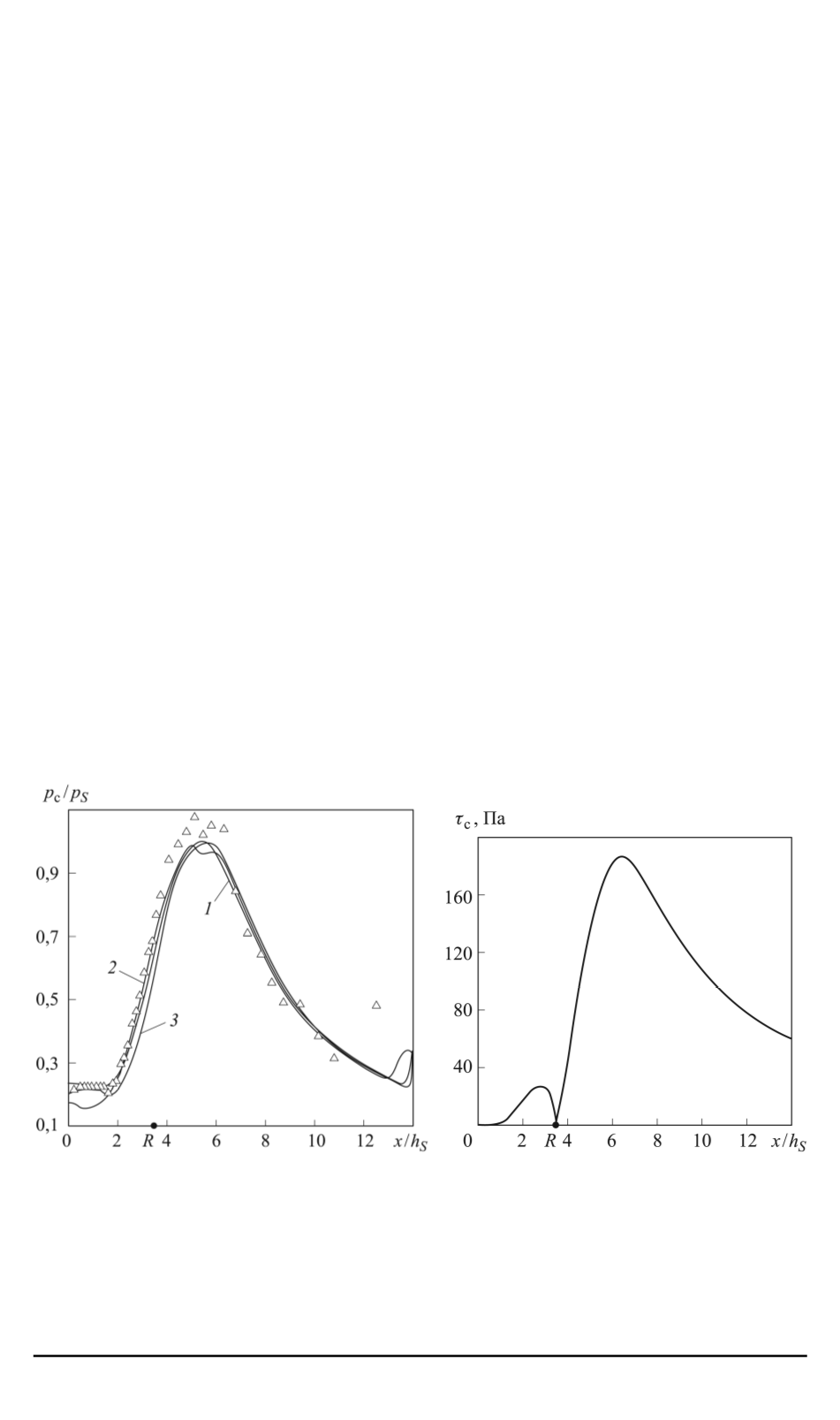
в области присоединения оторвавшегося пограничного слоя (рис. 6).
Распределение коэффициента теплоотдачи за уступом явно соот-
ветствует картине изменения давления на стенке: имеет место ярко
выраженный минимум в донной области и максимум по завершении
сжатия слоя смешения (рис. 7). Расчет теплоотдачи с помощью модели
Рис. 5. Сравнение экспериментальных
(точки) и расчетных (линии) распре-
делений давления на стенке за усту-
пом (
q
c
= 0
) для моделей турбулент-
ности
k
−
ε
(
1
),
k
−
ω
(
2
) и Спаларта –
Альмараса (
3
)
Рис. 6.
Распределение расчетного
касательного напряжения
τ
c
на
стенке за уступом для модели турбу-
лентности
k
−
ε
74
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 1


