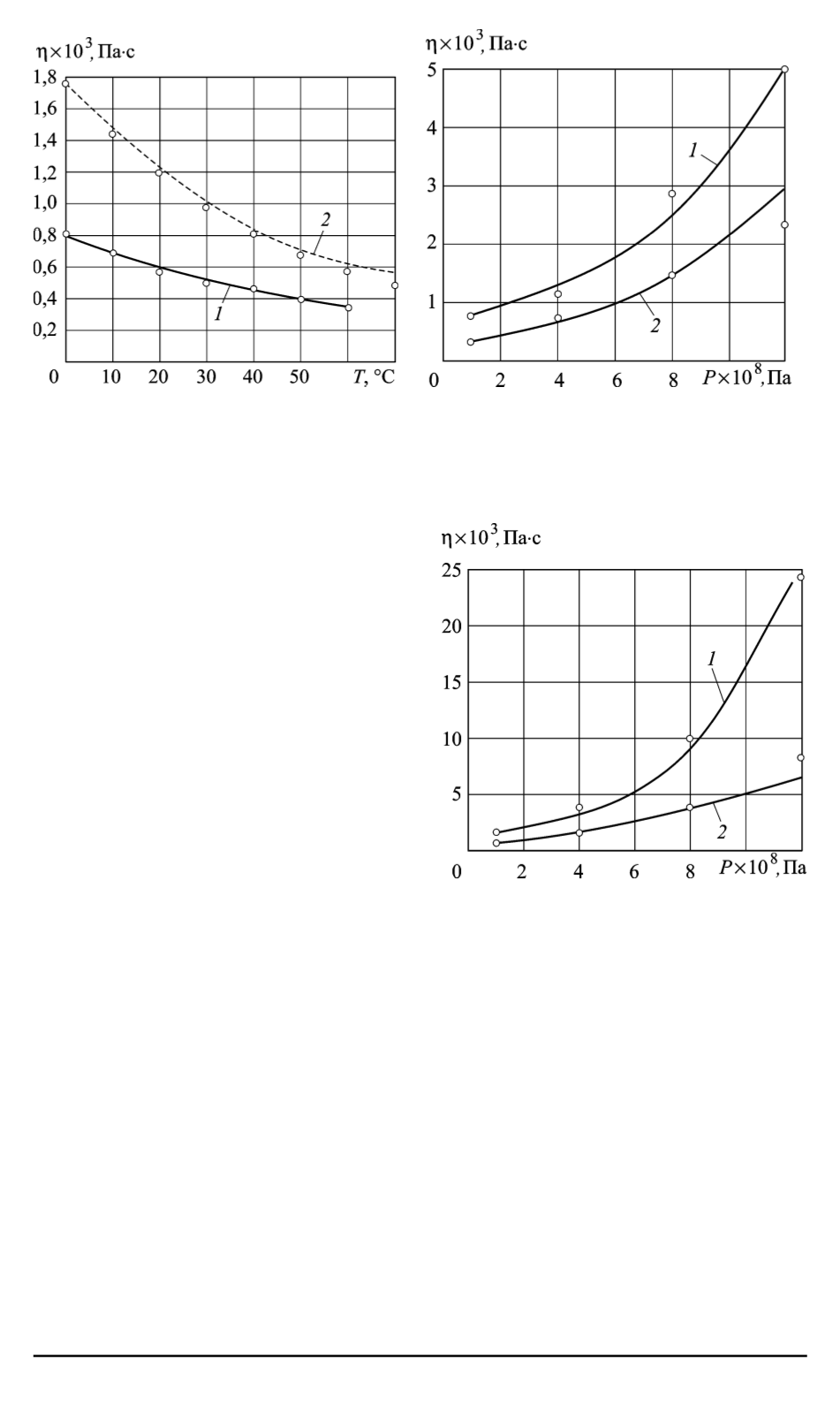
Рис. 1. Изобары жидкостей при атмо-
сферном давлении:
1
— спирт метиловый;
2
— спирт этило-
вый
Рис. 2. Изотермы метилового спирта:
теоретические (———) и эксперимен-
тальные (*,
◦
) значения для
T
= 30
(
1
)
и
75
◦
C (
2
)
Рис. 3. Изотермы этилового спирта:
теоретические (———) и эксперимен-
тальные (*,
◦
) значения для
T
= 30
(
1
)
и
75
◦
C (
2
)
газа величина
α
— бесконечно малая, ины-
ми словами, для реальных газов следует
полагать
α
= 0
.
Непосредственными вычислениями
для газов можно показать, что среднее
значение
β
=
−
2
,
3
∙
10
−
3
град
−
1
. Это под-
тверждает вывод, следующий из формулы
Сезерленда [4], о том, что вязкость газов
η
увеличивается с ростом
Т
.
Есть еще один случай состояния ве-
щества, заслуживающий особого рассмо-
трения — критическое состояние [5], кото-
рое характеризуется тем, что здесь исче-
зает всякое различие между жидкостью и
ее насыщенным паром (газом).
Выше отмечалось, что для жидкости
параметр
β >
0
, для газа
β <
0
и для
вещества в критическом состоянии
β
= 0
.
Из (1) следует, что для веществ в критиче-
ском состоянии параметр
γ
строго равня-
ется коэффициенту
η
динамической вязко-
сти этих веществ в критической точке.
В приложениях теории вязкости сме-
сей известен найденный эмпирически и
хорошо согласующийся с данными опыта закон Кендалла [2]. С его помощью уста-
навливается связь между значениями вязкости
η
Σ
раствора, эмульсии, суспензии и
значениями
η
j
отдельных
j
-х компонентов
(
j
= 1
,
2
, . . . N
)
. Закон Кендалла обычно
представляют в форме
ln
η
Σ
(
P, T
) =
N
X
j
=1
x
j
ln
η
j
(
P, T
)
,
(6)
где под коэффициентом
x
j
понимают молярную массу, весовую концентрацию или
относительный объем
j
-го компонента смеси. Если теперь полагать (1) справедли-
вым в общем случае, то все коэффициенты вязкости
η
j
могут быть заданы в форме
η
j
(
P, T
) =
γ
j
exp (
α
j
P
−
β
j
T
)
.
(7)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 3
117


