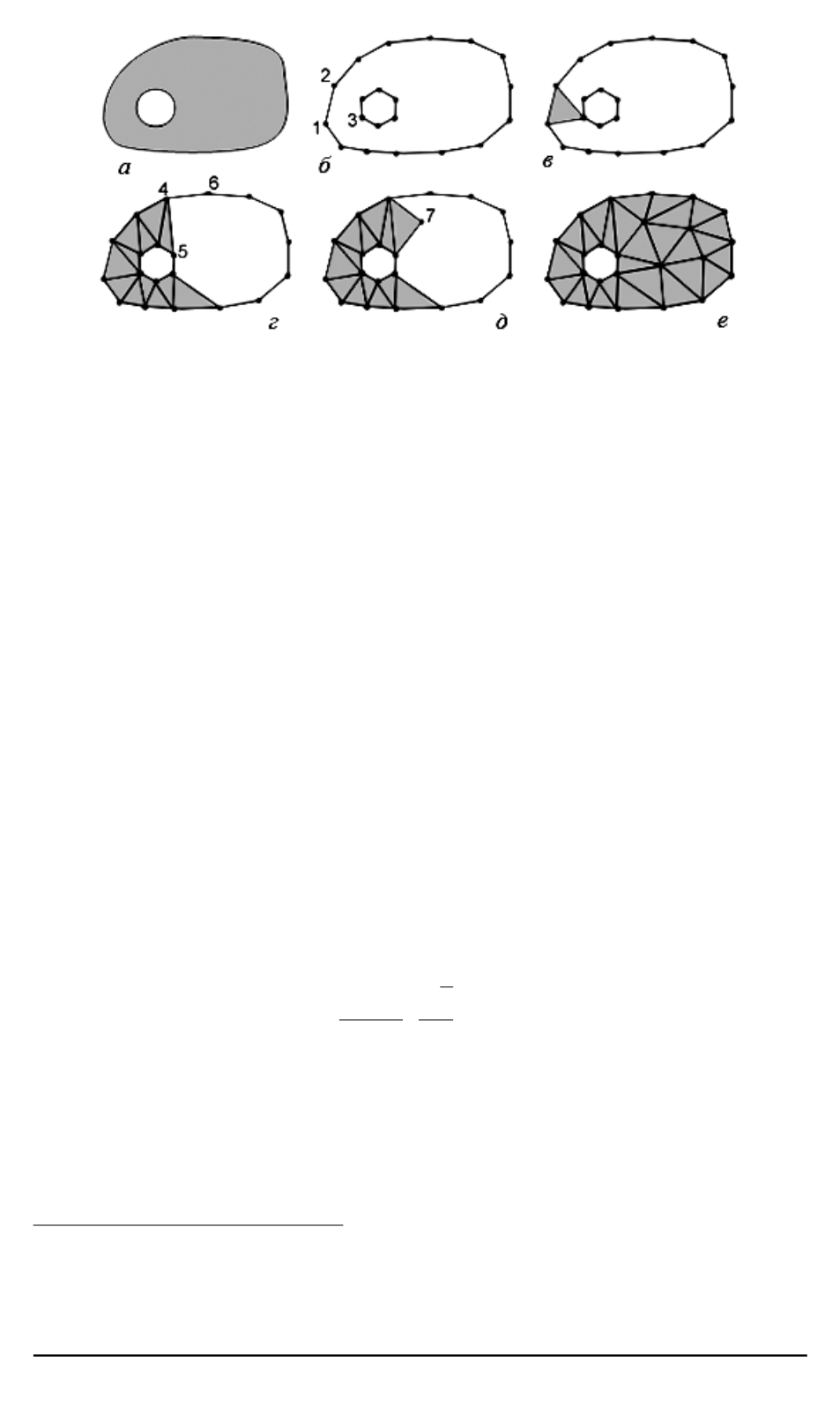
Рис. 1. Пример работы алгоритма исчерпывания в двумерном случае
рассматривается треугольник
T
(
g
1
, g
2
, g
3
)
и проверяются следующие
условия:
а)
Т
лежит в исчерпываемой области;
б) внутри и на границе
Т
нет никаких других узлов триангуляции,
кроме узлов, образующих этот треугольник;
в)
Т
не пересекается никакими ребрами существующей триангу-
ляции;
г) площадь (либо иная размерная характеристика)
Т
не превос-
ходит максимально допустимого условиями задачи значения. Среди
всех треугольников
Т
, удовлетворяющих указанным условиям, выби-
рается вариант с наилучшими аппроксимационными свойствами
1
[1]
и осуществляется переход к п. 5. Если же подходящих треугольников
не нашлось, то осуществляется переход к п. 4.
4. Поиск в исчерпываемой области точки
p
, для которой треуголь-
ник
T
(
g
1
, g
2
, p
)
удовлетворяет всем условиям из п. 3 и при этом облада-
ет лучшими аппроксимационными свойствами (т.е. в идеале на ребре
L
i
следует построить правильный треугольник). Для нахождения такой
точки достаточно восстановить из середины ребра
L
i
перпендикуляр
(высоту) длиной
h
= min
2
S
max
k
L
i
k
,
√
3
2
k
L
i
k
!
, где
S
max
— максимально
допустимая площадь элемента.
5. Обновление фронта по следующей схеме: рассматривается ка-
ждое ребро сформированного треугольника, и если ребро принадле-
жит фронту, то оно удаляется из фронта; если же ребро не принадле-
жит фронту, оно добавляется во фронт.
1
Аппроксимационные качества элемента зависят от его формы. В большинстве
методов наилучшими свойствами обладают правильные симплексы (т.е. правильные
треугольники и тетраэдры). Рассмотрение вариантов оценок этих свойств выходит
за рамки данной статьи.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2
97


