6. Если область еще не исчерпана, то выполняется п. 1, иначе
процесс окончен.
В приведенном на рис. 1 примере на первой итерации алгоритма
наименьшим углом обладает узел, обозначенный “1”. Согласно алго-
ритму, выбирается более длинное из двух ребер (1–2), а затем прово-
дится поиск среди граничных узлов, с которыми могут быть образо-
ваны подходящие элементы. Из них выбирается узел, позволяющий
создать треугольник с наилучшими аппроксимационными свойствами
(рис.1, фигура
в
). Далее итерации продолжаются, пока не реализуется
ситуация, иллюстрированная на рис. 1, фигура
г
. Здесь из фронта вы-
бирается ребро 4–5, однако с соседним узлом 6 элемент образовать
нельзя, так как его площадь получится слишком большой, поэтому
в область добавляется новый узел 7 (см. рис. 1, фигура
д
). Далее ал-
горитм продолжается до тех пор, пока вся область не оказывается
исчерпанной (т.е. пока множество ребер фронта
L
не станет пустым,
см. фиг.
в
на рис. 1).
Заметим, что самой ресурсоемкой частью любого алгоритма ис-
черпывания является проверка условий п. 3, так как необходимо удо-
стовериться, что новый элемент не пересекается ни с какими уже су-
ществующими. Причем на каждой итерации алгоритма эта процедура
с различными параметрами может вызываться от 5 до 20 раз (иногда
и больше). От того, каким образом выполнена эта проверка, главным
образом и зависит производительность алгоритма.
Реализация алгоритма исчерпывания в трехмерном случае та-
ит в себе несколько дополнительных трудностей (помимо очевидно
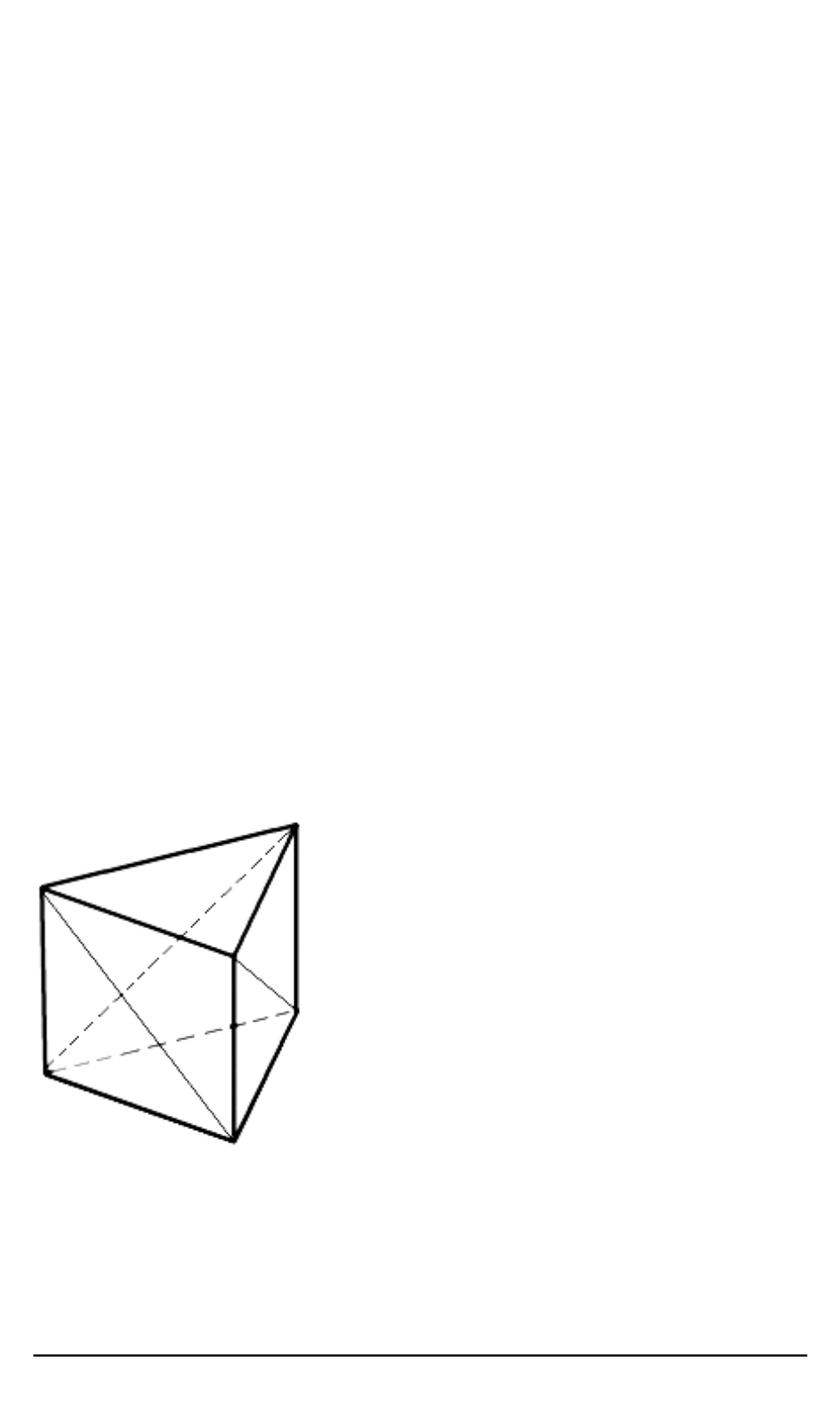
Рис. 2. Пример трехмерной
области (пятигранная приз-
ма), которую невозможно
разбить на тетраэдры без
вставки дополнительного
узла
большей ресурсоемкости). В первую оче-
редь следует отметить краеугольную про-
блему трехмерной дискретизации: нередка
ситуация, когда в результате работы алго-
ритма образуются области, которые невоз-
можно дискретизировать, не используя до-
полнительных внутренних узлов (пример
такой ситуации приведен на рис. 2). В дву-
мерном случае этой проблемы нет, так как
любой многоугольник на плоскости мож-
но разбить на треугольники одними толь-
ко внутренними ребрами. Вторая главная
сложность связана с выбором текущей гра-
ни фронта для построения тетраэдра. Де-
ло в том, что для этого весьма желатель-
но использовать грань, вершинами которой
являются узлы с наименьшими значениями
98
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2


