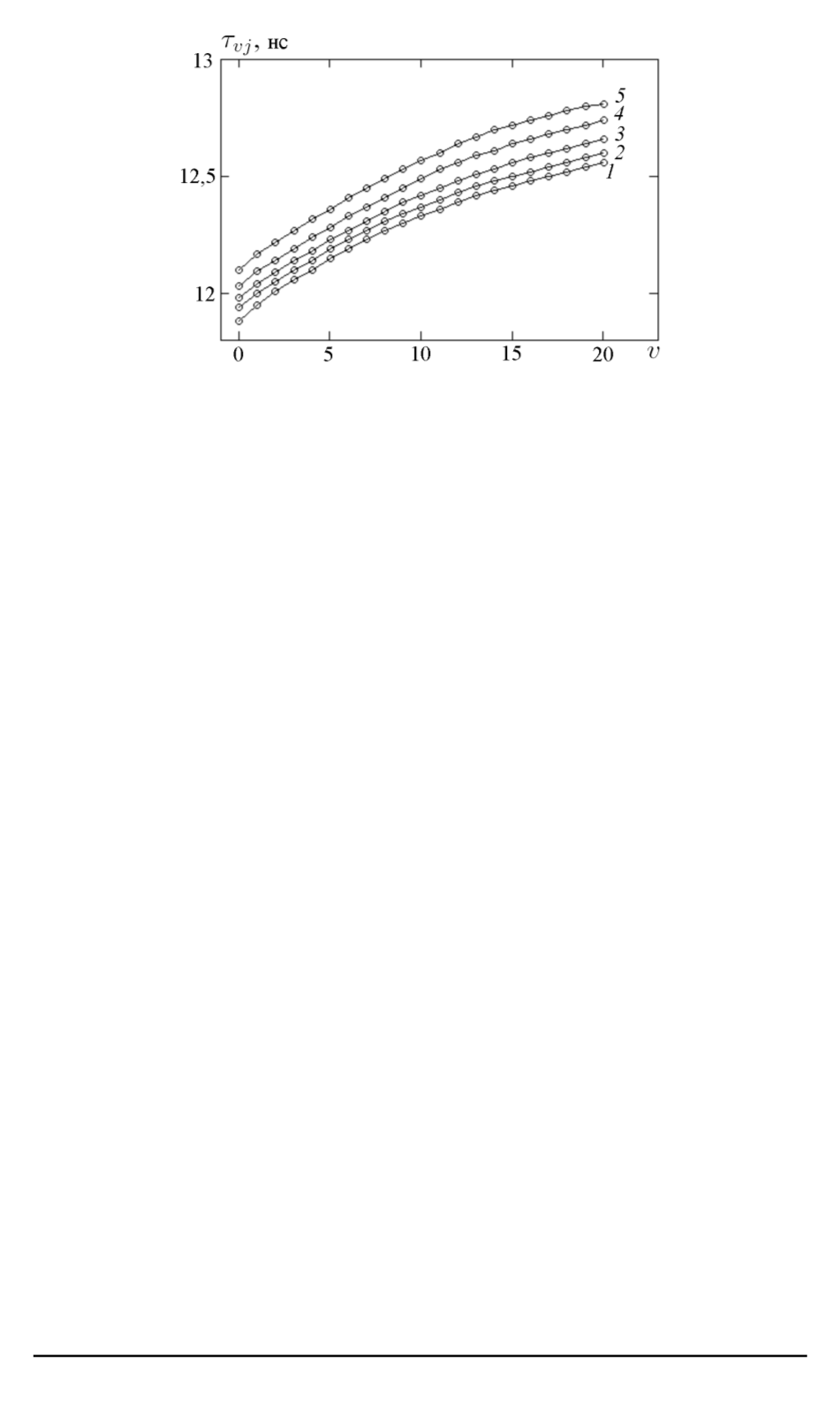
Рис. 5. Результаты расчета радиационных времен жизни колебательно-
вращательных уровней
B
1
Π
u
-состояния
39
K
2
:
j
= 0
(
1
);
j
= 43
(
2
);
j
= 61
(
3
);
j
= 80
(
4
);
j
= 100
(
5
)
j
0
= 43
,
59
,
61
;
v
00
≤
32
) в спектре лазерно-индуцированной флуо-
ресценции перехода
B
1
Π
u
−
X
1
Σ
+
g
молекулы
39
K
2
. Рассчитанные в
данной работе волновые числа вращательных линий в пределах экс-
периментальных погрешностей хорошо согласуются с измерениями
в спектре. Экспериментальные измерения времени жизни состояния
B
1
Π
u
проводились разными методами в работах [22, 23]. В работе [22]
использовали метод фазового сдвига. Было измерено среднее значение
τ
v
= 12
,
4
±
0
,
3
нс для колебательных уровней
v
= 6
,
7
и 8, которое хо-
рошо согласуется с результатами расчета данной работы (см. рис. 5).
Расчеты
τ
v,j
=0
, выполненные в работе [22] для
v
≤
13
, хорошо согласу-
ются с результатами настоящей работы. Различия не превышают 1%.
В работе [23] для измерения времени жизни состояния
B
1
Π
u
исполь-
зовали счетчик фотонов с высоким временным разрешением. Было
определено среднее время жизни
τ
(
B
1
Π
u
) = 12
,
2
±
0
,
2
нс. Рассчитан-
ное в настоящей работе среднее значение времени жизни состояния
B
1
Π
u
для
j
0
= 0
,
v
0
≤
20
, равное
12
,
2
±
0
,
3
нс, хорошо согласуется с
измеренным значением.
В настоящей работе впервые получены коэффициенты Эйнштейна,
силы осциллятора для электронного перехода
A
1
Σ
+
u
−
X
1
Σ
+
g
и ради-
ационные времена жизни колебательно-вращательных уровней возбу-
жденного состояния
39
K
2
. Так как при расчете времен жизни состо-
яния
B
1
Π
u
использовались коэффициенты Эйнштейна, полученные
в данной работе, то на основании хорошо согласующихся экспери-
ментальных и рассчитанных времен жизни можно сделать вывод о
надежности коэффициентов Эйнштейна.
Полные данные по рассчитанным радиационным параметрам и
временам жизни возбужденных состояний для переходов
A
1
Σ
+
u
−
X
1
Σ
+
g
и
B
1
Π
u
−
X
1
Σ
+
g
молекулы
39
K
2
могут быть получены от автора.
82
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 2


