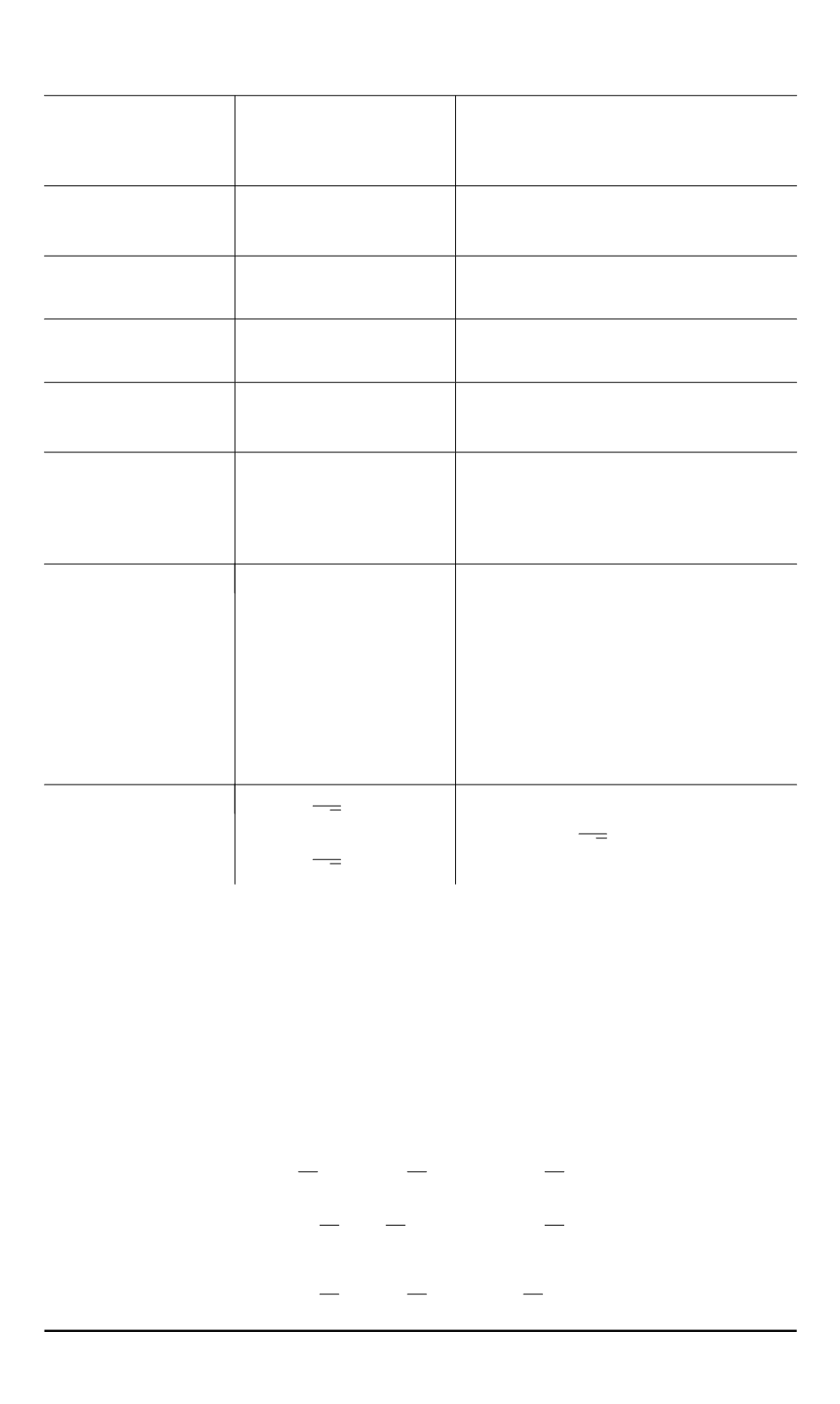
Таблица 2
Преобразования квантовых вентилей
Название, обозна-
чение и краткое
описание квантово-
го вентиля
Действие на базовые
состояния
Матрица
Тождественное пре-
образование
I
|
0
i → |
0
i
|
1
i → |
1
i
1 0
0 1
!
Отрицание
X
|
0
i → |
1
i
|
1
i → |
0
i
0 1
1 0
!
Фазовый сдвиг
Z
|
0
i → |
0
i
|
1
i → − |
1
i
1 0
0
−
1
!
Фазовый сдвиг с от-
рицанием
Y
|
0
i → − |
1
i
|
1
i → |
0
i
0 1
−
1 0
!
Controlled-NOT
CNOT
Прибавляет ко вто-
рому биту первый
по модулю 2
|
00
i → |
00
i
|
01
i → |
01
i
|
10
i → |
11
i
|
11
i → |
10
i
1 0 0 0
0 1 0 0
0 0 0 1
0 0 1 0
Controlled-
Controlled NOT
(Вентиль Тофолли)
Прибавляет к тре-
тьему биту произ-
ведение двух пер-
вых (по модулю
два).
|
000
i → |
000
i
|
001
i → |
001
i
|
010
i → |
010
i
|
011
i → |
011
i
|
100
i → |
100
i
|
101
i → |
101
i
|
110
i → |
111
i
|
111
i → |
110
i
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 0
Преобразование
Адамара
H:
|
0
i →
1
√
2
(
|
0
i
+
|
1
i
)
|
1
i →
1
√
2
(
|
0
i − |
1
i
)
1
√
2
1 1
1
−
1
!
квантовым битом регистра; 2) инверсия относительно среднего. Это
преобразование можно записать следующим образом:
X
i
|
t
i
i →
X
i
(2
a
ср
−
a
i
)
|
t
i
i
,
где
a
ср
— средняя амплитуда.
Инверсию относительно среднего можно записать в виде матрицы
D
=
2
N
−
1
2
N
. . .
2
N
2
N
2
N
−
1
∙ ∙ ∙
2
N
∙ ∙ ∙
∙ ∙ ∙
∙ ∙ ∙
∙ ∙ ∙
2
N
2
N
∙ ∙ ∙
2
N
−
1
.
116
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 2


