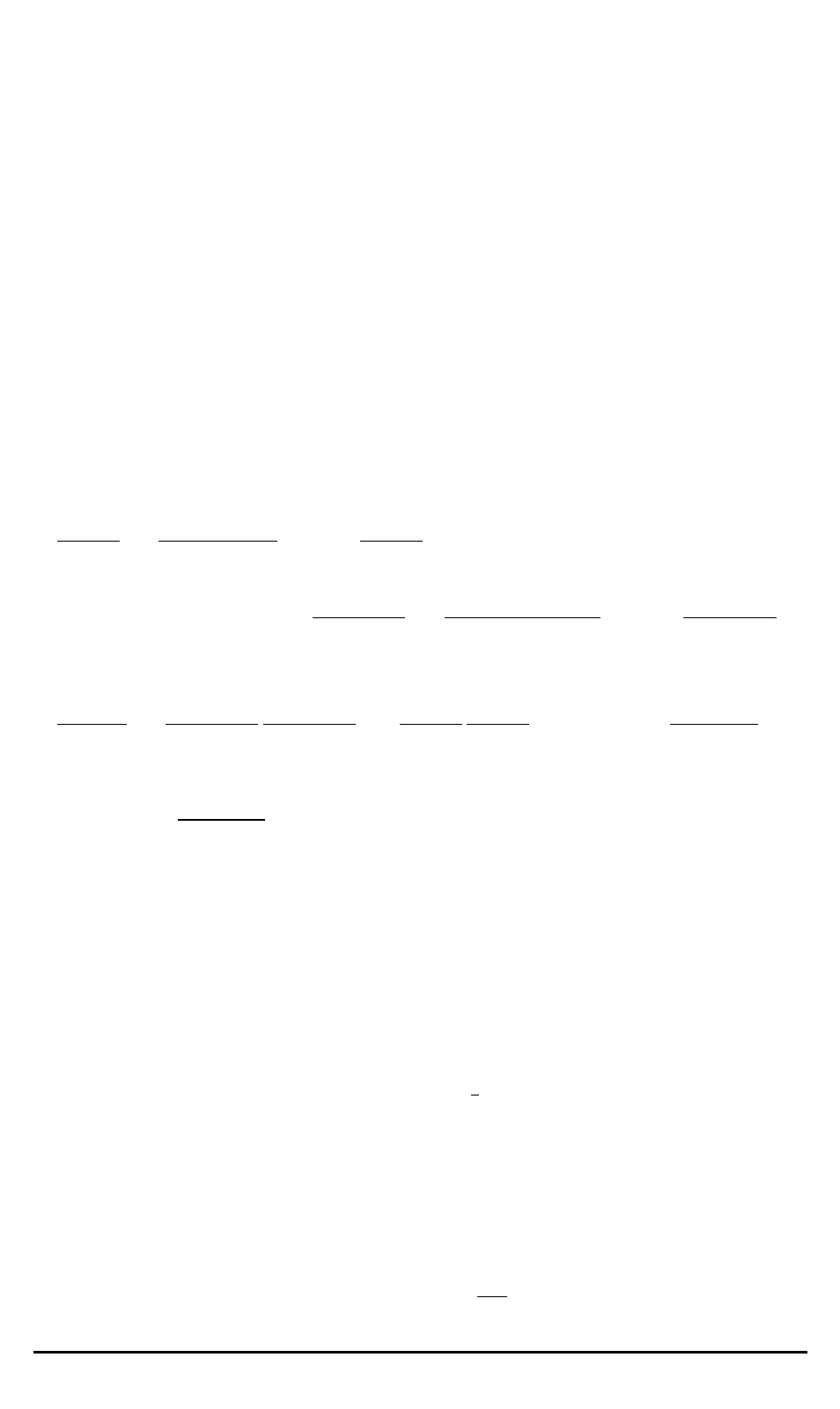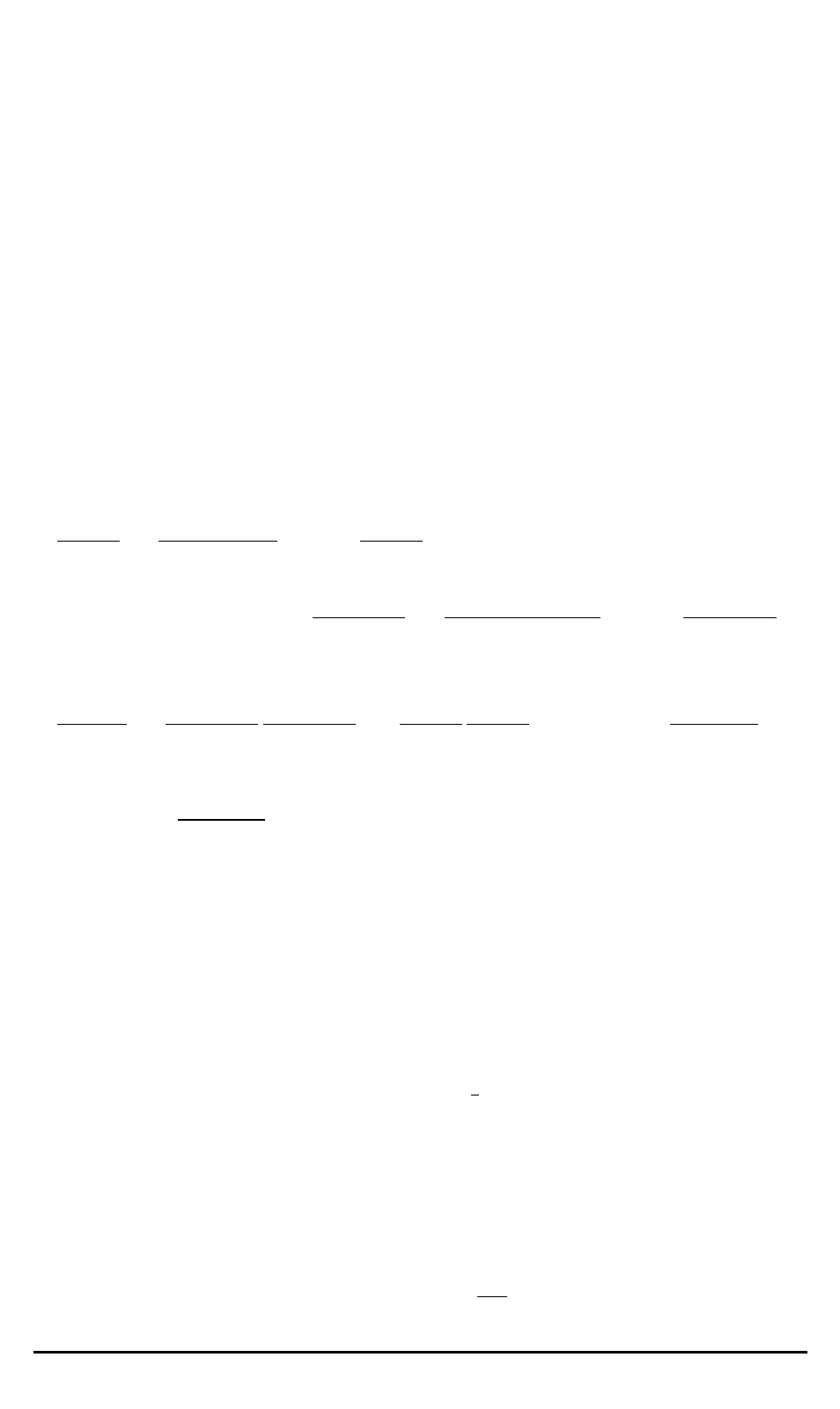
basis for
L
2
(Ω)
. Notice
E
⊂
B
n
, by Lemma 1, it implies
0 = sup
B
n
F
∞
,
α
ψ
α
≥
sup
E
F
∞
,
α
e
γ
α
α
0
.
Which means all Fourier coefficients of
F
∞
are zero, hence
F
∞
= 0. Then
(13) holds in the sense
F
0
2
=
∞
β
=1
λ
2
β
.
(15)
Now we proceed to justify the second statement claimed in the Theorem
about the convergence rapidity of the expansion (15). By assumption all
F
β
=
0, and due to (10) and (11), the following relations and the continuous
multiplication are well defined,
F
1
2
F
0
2
=
F
0
2
−
λ
2
1
F
0
2
= 1
−
λ
2
1
F
0
2
,
· · ·
· · ·
,
F
N
2
F
N
−
1
2
=
F
N
−
1
2
−
λ
2
N
F
N
−
1
2
= 1
−
λ
2
N
F
N
−
1
2
,
F
N
2
F
0
2
=
F
N
2
F
N
−
1
2
F
N
−
1
2
F
N
−
2
2
· · ·
F
2
2
F
1
2
F
1
2
F
0
2
=
N
β
=1
1
−
λ
2
β
F
β
−
1
2
.
Denote
α
2
β
=
λ
2
β
F
β
−
1
2
, namely
λ
β
=
α
β
F
β
−
1
. By the proved previously,
0
< α
β
≤
1
, and notice that the inequality
(1
−
α
)
≤
e
−
α
always holds,
then we have
F
N
2
=
F
0
2
N
β
=1
(1
−
α
2
β
)
F
0
2
e
−
N
β
=1
α
2
β
,
or
F
N
≤
F
0
e
−
1
2
N
β
=1
α
2
β
.
(16)
Let
R
N
+1
=
F
N
2
=
∞
β
=
N
+1
λ
2
β
be the sum of residual part of (15). It is
easy to show the sum
N
k
=1
α
2
k
=
N
k
=1
λ
2
k
R
k
42
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2005. № 4