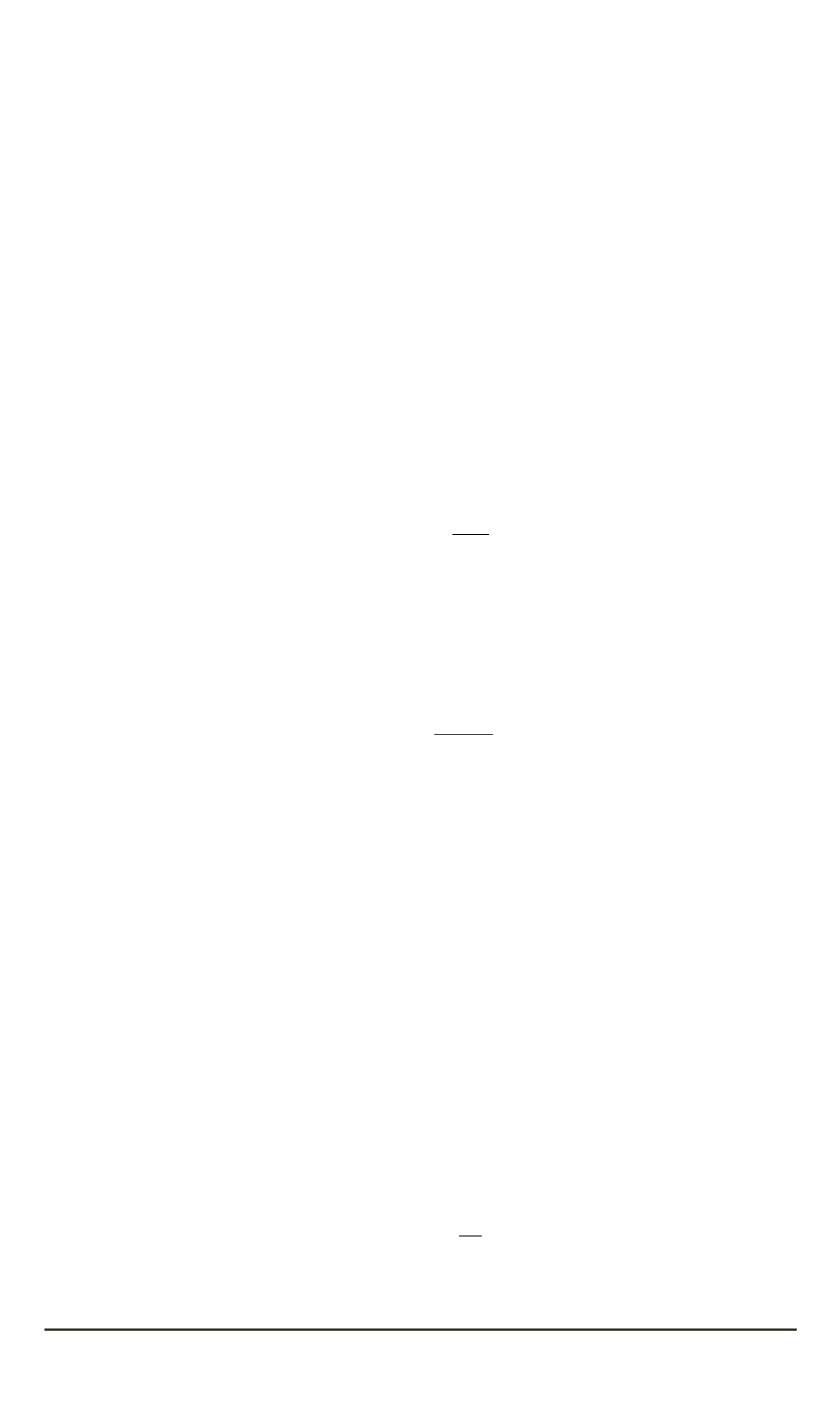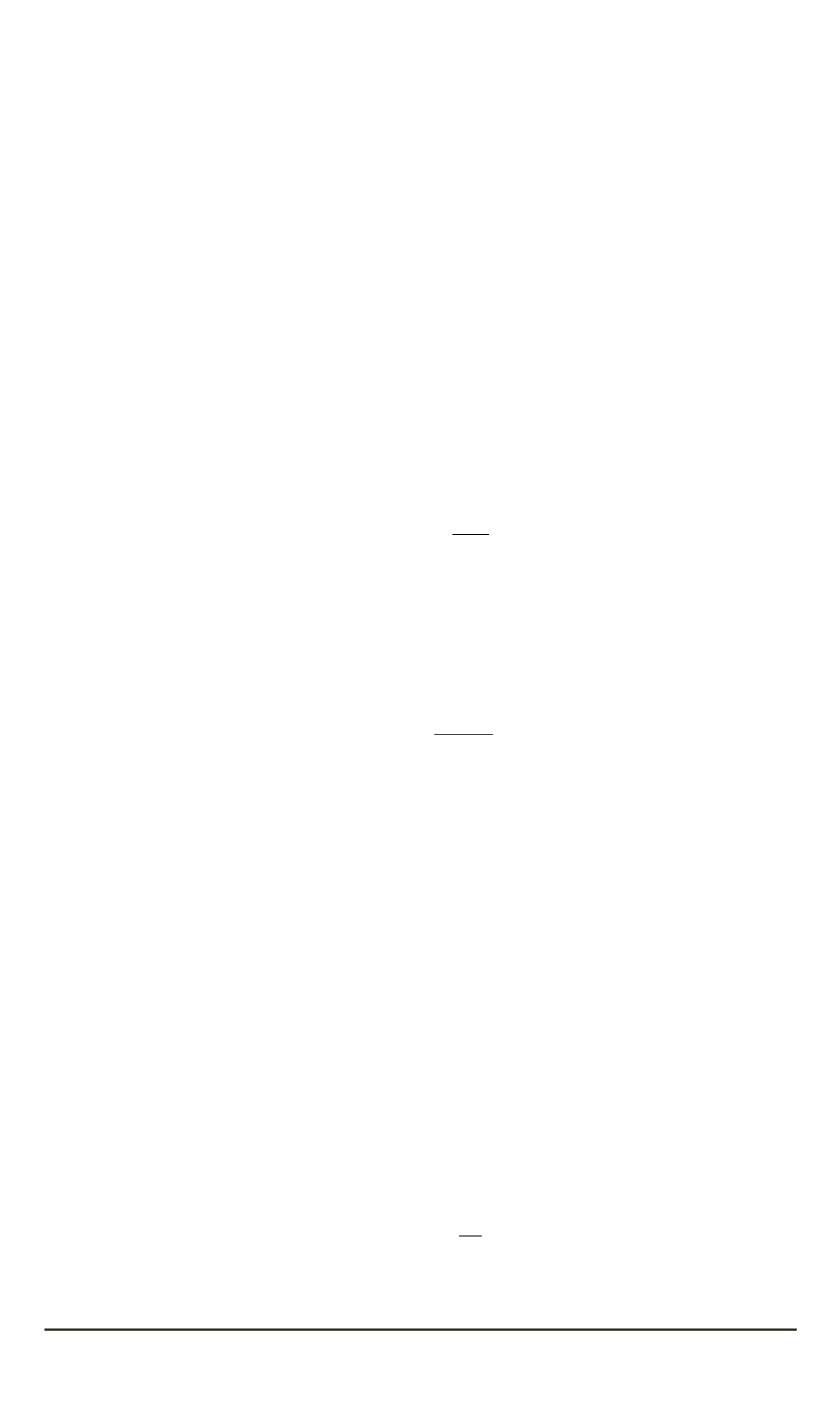
взрыва космического тела связана с поражающим действием вызван-
ной взрывом гравитационной волны. Возникающие нагрузки на эле-
менты риска определяются суммарным действием скоростного напора
и гидростатического давления. Масса космического тела определяется
по его плотности и линейному размеру как диаметру сферы. Меха-
нический эквивалент энергии взрыва принимается с коэффициентом
K
п
= 0
,
6
.
Расчет основан на данных, полученных экспериментально при под-
водных ядерных взрывах [6]. Основными расчетными параметрами
водяных гравитационных волн являются высота волны и ее скорость,
изменяющиеся со временем при распространении на континенталь-
ном шельфе и далее на прибрежной территории. Экспериментальная
информация представлена в функции параметров подводного взрыва
от глубины и эпицентрального расстояния энергетического источника
с тротиловым эквивалентом
W
1
= 1
кт. Пересчет высоты волны на
иную мощность взрыва осуществляется по формуле закона подобия
H
=
H
1
3
√
W
2
,
где
Н
1
= 20
м;
W
— мощность взрыва, кт, с учетом энергетической
доли по образованию волны
K
п
= 0
,
6
.
На урезе воды (береговой линии) высота волны
h
ур
определяется
по формуле
h
ур
= 1
,
3
H
B
п
B
мелк
1
/
4
,
где
Н
— начальная высота волны в месте падения космического тела в
акваторию;
В
п
— глубина воды в месте падения;
В
мелк
— глубина воды
в прибрежной отмели.
Для определения скорости
С
, м/с, распространения волн исполь-
зуют формулу Лагранжа [7], согласующуюся с данными наблюдений
за волнами цунами в Тихом океане:
C
=
p
2
gH .
Здесь
g
— ускорение свободного падения, м/с
2
;
Н
— глубина океана, м.
Время распространения волн от эпицентра до берега определяется
с учетом расстояния от места падения космического тела до берега и
скорости распространения волн.
Давление гидравлического потока в основном зависит от скоро-
сти потока по берегу. Скорость распространения потока у уреза воды
U
ур
, м/с, приблизительно можно определить по формуле [7]
U
ур
=
β
√
H,
где
β
= 3
— константа, м
1
/
2
/
с.
130
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 6