
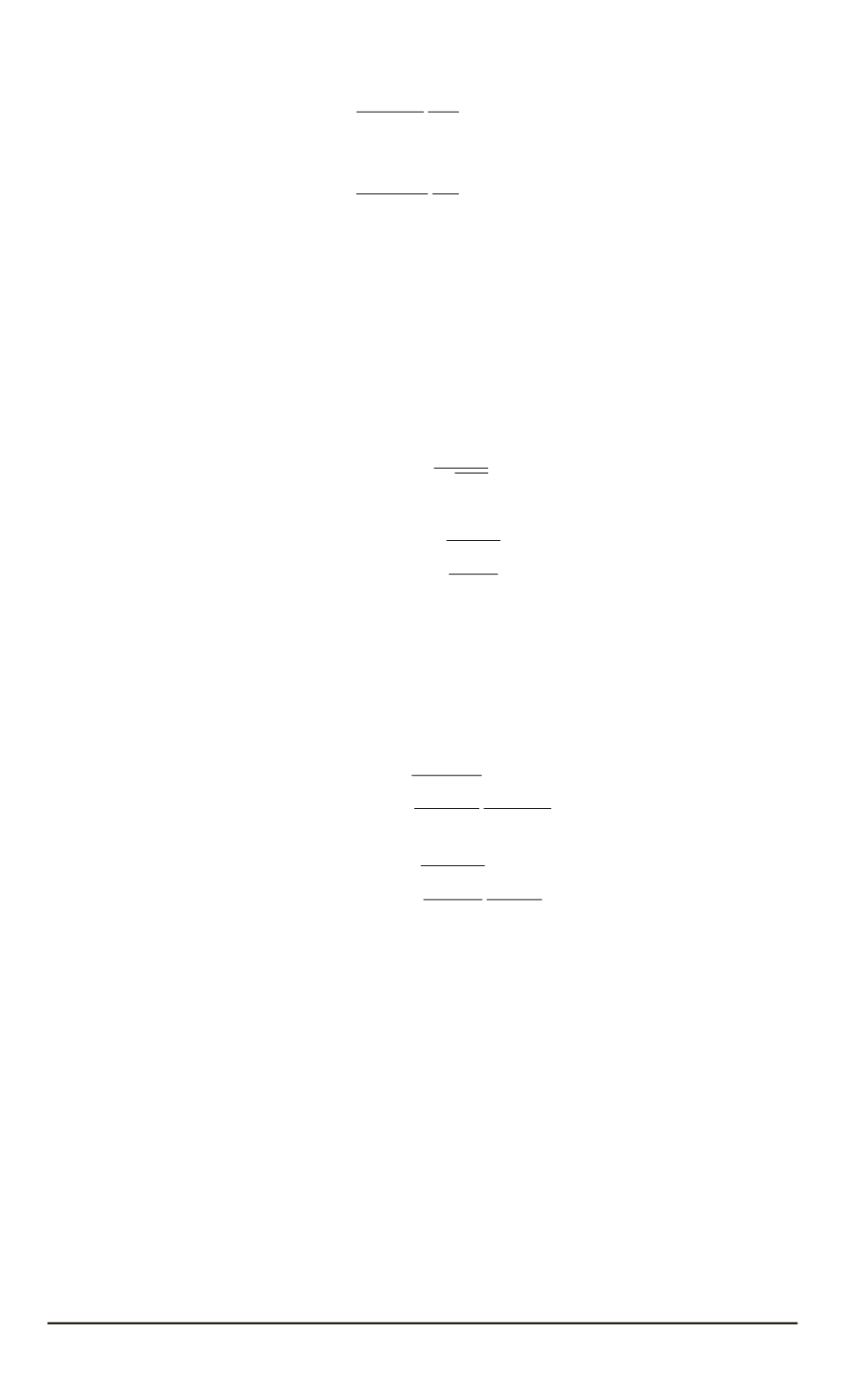
описывается формулой (13), при
ω β
имеет вид
δG
∗
W
=
36
k
e
c
3
9
L
2
~
Δ
2
ω
4
W
0
G
h
(
ω
)
,
или
δG
∗
W
=
8
k
e
cL
2
9
~
β
2
ω
4
W
0
G
h
(
ω
)
.
(17)
Сравнения формул (15) и (17) позволяет сделать вывод, что использо-
вание низкочастотного оптического резонанса при регистрации высо-
кочастотных гравитационно-волновых возмущений существенно по-
вышает чувствительность лазерных гравитационных антенн.
Условием наблюдения гравитационно-волнового сигнала при
усреднении спектральной плотности за период времени
T
являет-
ся неравенство
δG
W
>
1
√
βT
,
или с учетом (5) и (7)
δG
W
>
r
2
L
cT
Δ
.
(18)
Подстановка формул (14) и (15) в неравенство (18) дает выражение
для оценки минимальной спектральной плотности флуктуаций метри-
ки пространства – время, которая может быть зарегистрирована с по-
мощью предлагаемого интерферометра Фабри – Перо, использующего
явление низкочастотного оптического резонанса:
G
h
(
ω
)
>
r
2
c
TL
3
Δ
~
κ
2
4
k
e
W
0
,
(19)
или
G
h
(
ω
)
>
r
2
L
c
3
T
Δ
~
ω
2
k
e
W
0
.
Для случая фазовой настройки интерферометра Фабри – Перо
κ
= 0
,
1
и при параметрах лазерной гравитационной антенны
Δ = 10
−
4
,
L
= 100
м,
W
0
= 10
3
Вт,
T
= 10
7
с (116 сут.) и
k
e
= 5
,
9
∙
10
6
м
−
1
(
λ
e
= 1
,
064
мкм), из выражения (19) имеем минимально обнаружива-
емую спектральную плотность флуктуаций гравитационно-волнового
возмущения
G
h
(
ω
)
>
3
,
5
∙
10
−
49
с. При этом циклическая часто-
та такого возмущения в соответствии с формулой (16) будет равна
ω
= 1
,
5
∙
10
5
с
−
1
.
Отметим, что аналогичную чувствительность можно получить и
для случая уменьшения длины интерферометра в 10 раз (
L
= 10
м),
при этом фазовую настройку интерферометра необходимо будет изме-
нить до значения
κ
= 1
,
77
∙
10
−
2
, а циклическая частота станет равной
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 1
31

















