
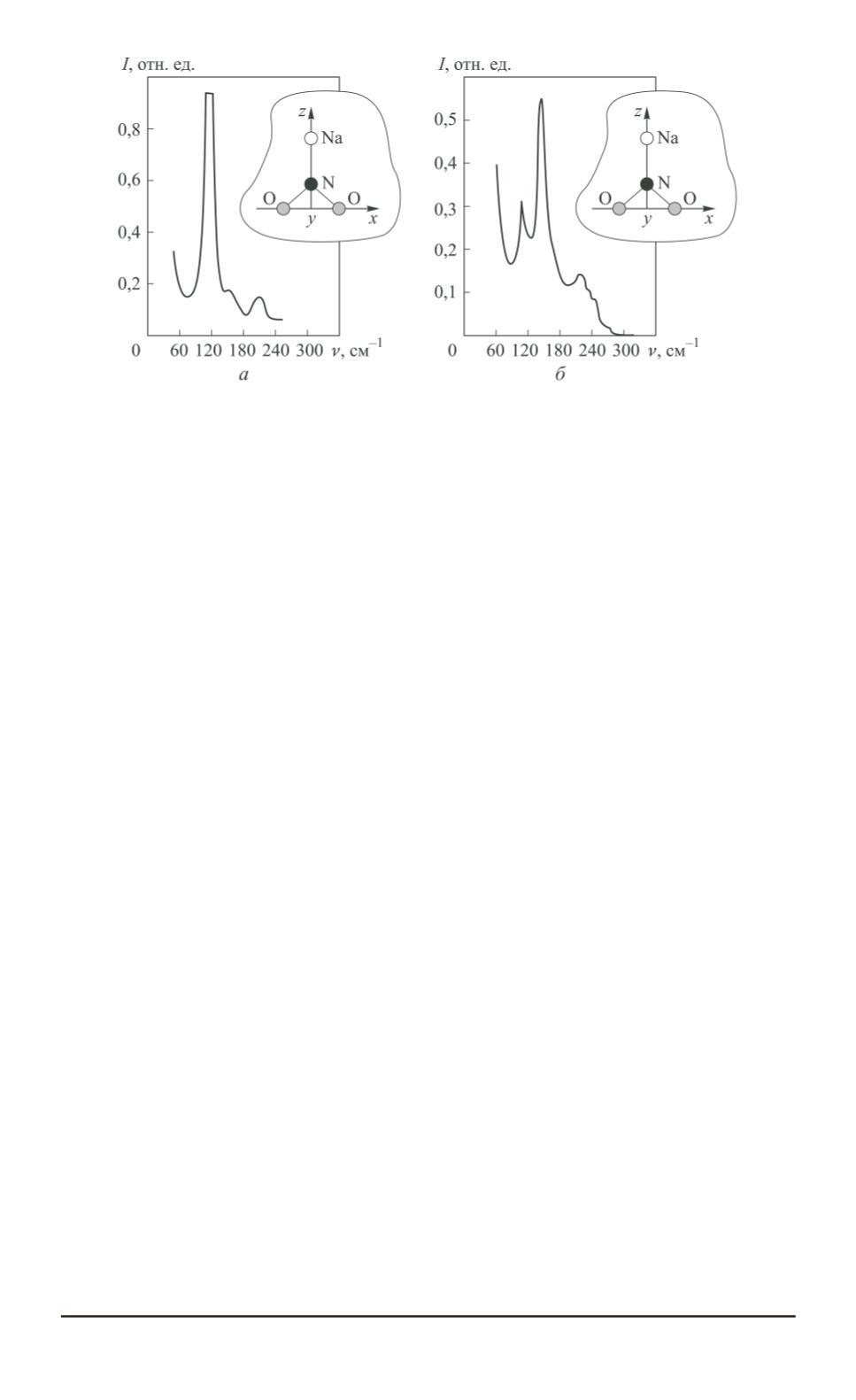
Рис. 3. Вид спектров комбинационного рассеяния света в монокристаллах
нитрита натрия, полученных для двух геометрий рассеяния
z
(
xy
)
x
(
а
) и
y
(
xz
)
x
(
б
) (псевдоскалярная мода проявляется при геометрии
z
(
xy
)
x
)
псевдоскалярной симметрией (как и аксионы вакуума). Такая мода со-
ответствует поворотным качаниям (twist-like mode, или твист-мода)
группы NO
2
около оси
z
(см. рис. 2). Без наложения внешнего магнит-
ного поля для обсуждаемого кристалла процесс фотон-аксионной кон-
версии запрещен, так как представление
A
2
не содержится в векторном
представлении
V
(см. табл. 2). В то же время для двухфотонного про-
цесса типа комбинационного рассеяния
([
V
]
2
= 3
A
1
+
А
2
+
В
1
+
В
2
;
[
V
]
2
T
А
2
6
=
∅
)
процесс конверсии разрешен. Следует отметить, что
в спектрах комбинационного рассеяния света монокристаллов нитри-
та натрия псевдоскалярная либрационная мода, проявляющаяся при
геометрии рассеяния
z
(
xy
)
x
(см. табл. 2), имеет наибольшую интен-
сивность и характеризуется высокой добротностью (рис. 3).
При проникании аксионов из вакуума в кристалл нитрита на-
трия должна происходить гибридизации вакуумной и решеточной
мод одинаковой симметрии (псевдоскалярного типа), аналогичная
поляритонной гибридизации. Для описания дисперсионных кривых,
возникающих в кристалле в результате такой гибридизации, исполь-
зуем уравнения, аналогичные уравнениям (3):
¨
w
=
−
ω
2
ps
w
+
ω
2
ips
η
;
¨
η
=
−
ω
2
a
η
−
c
2
0
k
2
η
−
¨
w
.
Параметр
w
относится к псевдоскалярной моде вещества, параметр
η
— к аксионам вакуума, а частоты
ω
a
,
ω
ps
,
ω
ips
задают соответствую-
щие значения для аксионов, либрационной моды и их взаимодействия.
Вид дисперсионных кривых для этого случая показан на рис. 4.
В отличие от поляритонного эффекта, в рассматриваемом случае
нижняя ветвь начинается не в начале координат, а с конечного зна-
чения частоты. Это связано с тем, что масса покоя аксиона отлична
от нуля. Квазичастицы, возникающие в результате гибридизации ак-
сионов с псевдоскалярными оптическими фононами, будем называть
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 4
29

















