
Моделирование и метод расчета кавитационно-вихревого аппарата
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 1
85
где
вх
p
— давление жидкости при входе в сопло;
i
p
— давление жидкости в ра-
бочей части сопла.
Эффективность работы форсунки зависит от физических параметров
жидкости, проходящей через сопло, поэтому формулой (5) целесообразно свя-
зывать основные параметры потока жидкости в рабочей части сопла форсунки
и параметры подводимого потока. Таким образом, скорость жидкости в рабо-
чей части сопла находят по формуле
вх с
ж
2 2
ж
2(
)
,
(1
cos )
p p
V
k
где
k
— степень изменения проходного сечения рабочей части сопла форсунки;
— угол отклонения вектора скорости на выходе из форсунки от радиально-
осевого направления;
p
с
— давление жидкости в рабочей части сопла.
Для центробежных форсунок тангенс угла раскрытия факела равен отноше-
нию тангенциальной и осевой составляющих вектора скорости. В предлагаемом
устройстве большое влияние на выход жидкости из сопла оказывает радиальная
составляющая скорости, полученная потоком в корпусе форсунки, поэтому ми-
нимальный угол раскрытия факела распыла определяют по формуле
2arccos cos cos .
2
Угол раскрытия факела распыла увеличивается при увеличении угла рас-
крытия срединной конической поверхности канала в корпусе форсунки.
Аналогичная зависимость рассматриваемого параметра наблюдается от угла
отклонения вектора скорости на выходе из форсунки от радиально-осевого
направления, при этом, чем выше интенсивность закрутки потока, тем меньшее
влияние на раскрытие факела оказывает угол раствора срединной поверхности
канала.
Согласно зависимости, приведенной на рис. 2, закручивающее устройство в
корпусе форсунки следует устанавливать при небольшом угле раствора средин-
ной поверхности канала.
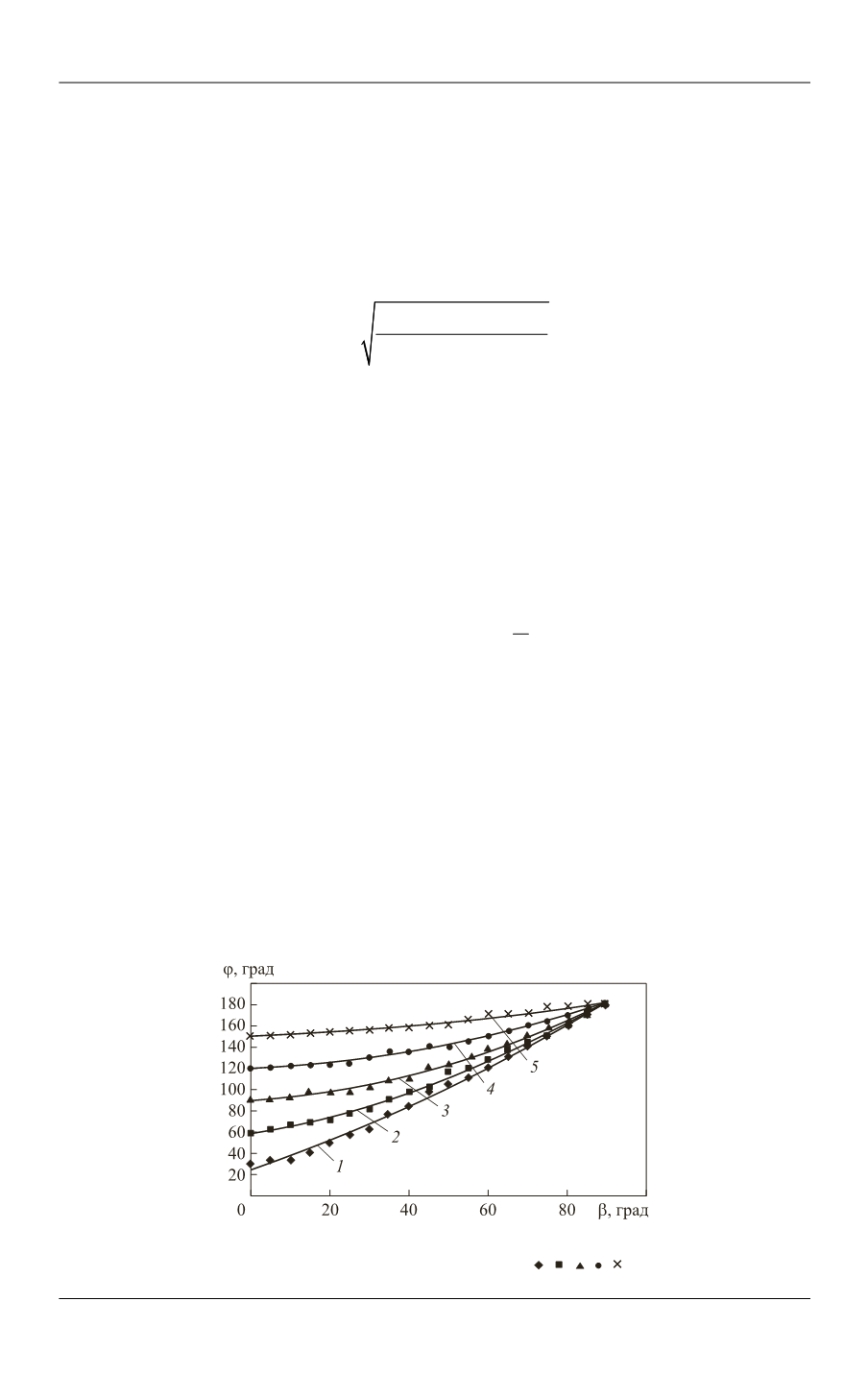
Рис. 2.
Зависимость минимального угла φ раскрытия факела от угла отклонения
при
= 30
(
1
), 60
(
2
), 90
(
3
), 120
(
4
) и 150
(
5
) ( , , , ,
— эксперимент)
















