
А.Д. Смирнов
70
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
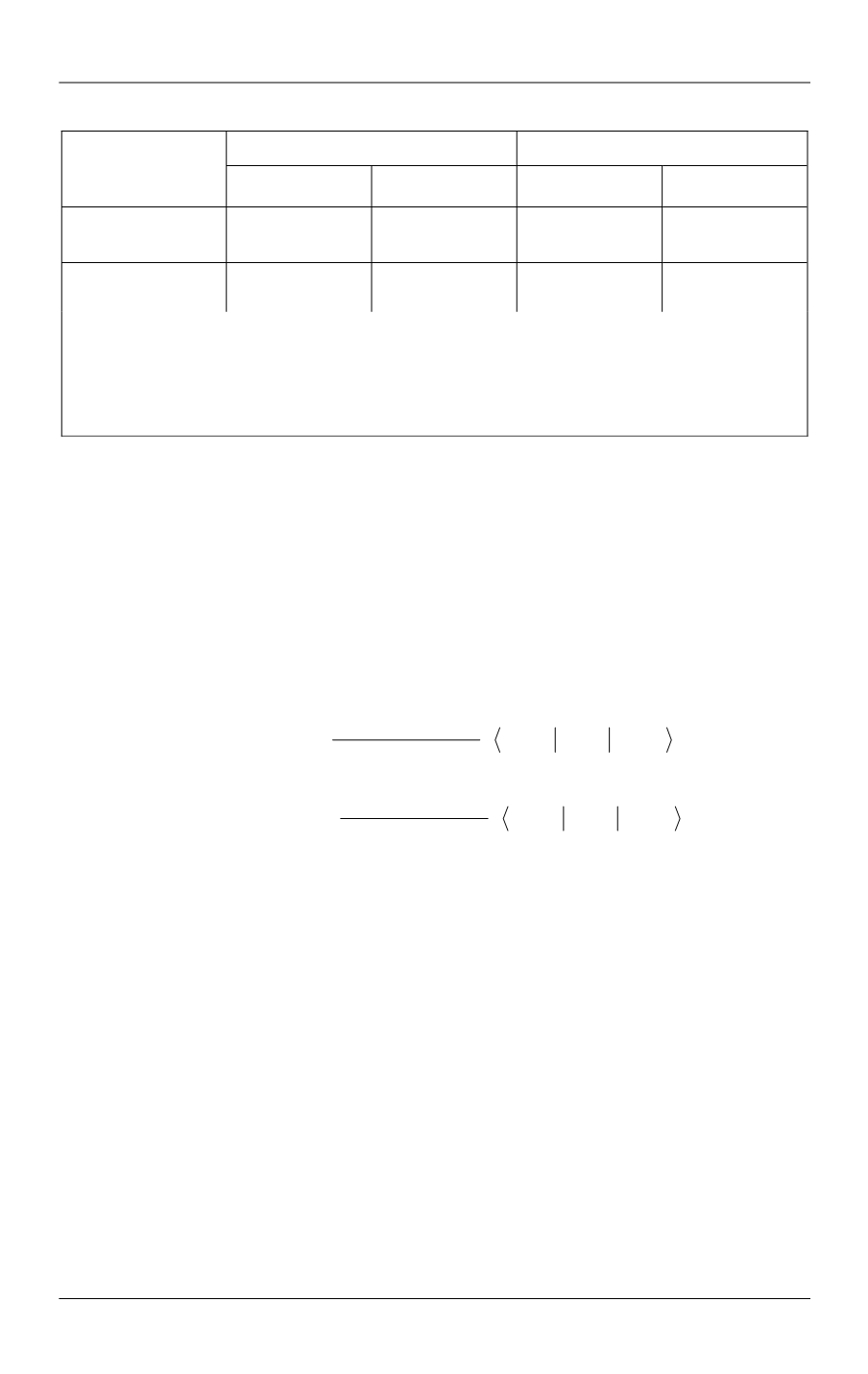
Окончание табл. 1
Молекулярные
постоянные
CsLi
+
KLi
+
X
2
2
(2)
X
2
2
(2)
e
D
6,836(–7)**
6,847(–7)
1,752(–7)**
1,757(–7)
1,176(–6)**
1,178(–6)
2,520(–7)**
2,519(–7)
e
H
6,96(–13)***
6,69(–13)
1,37(–13)***
1,38(–13)
1,71(–12)***
1,67(–12)
5,52(–15)***
5,44(–15)
Примечания.
В первой строке приведены данные, взятые из работ [14, 15], во второй
строке — значения, рассчитанные на основе потенциальных кривых. * — расчет по соотноше-
нию (1) с использованием литературных данных; ** — расчет по соотношению (2) с использо-
ванием литературных данных; *** — расчет по соотношению (3) с использованием литератур-
ных данных. В скобках приведен десятичный порядок величины.
Расчет радиационных параметров.
К радиационным параметрам относят-
ся коэффициенты Эйнштейна для спонтанного излучения
,
v v
A
силы осцилля-
тора
,
v v
f
факторы Франка — Кондона
,
v v
q
волновые числа электронно-
колебательных полос
,
v v
времена жизни колебательных уровней возбужден-
ного электронного состояния
,
v
функция дипольного момента электронного
перехода от межъядерного расстояния
( ).
e
R r
Коэффициент Эйнштейна, с
–1
, и сила осциллятора для поглощения (безраз-
мерная величина) связаны с функцией
( ),
e
R r
ат. ед., соотношениями [20]
3
0,
2
0,
6
(2
)
( ) ( ) ( ) ;
(2
2, 6 0
)
02 1
v v
v v
v
e
v
A
r R r
r
(4)
0,
погл
2
0,
6
(2
)
( ) ( ) ( ) ,
(2
)
3, 0376 10
v v
v
e
v
v v
f
r R r
r
(5)
где Λ — проекция орбитального момента количества движения электронов на
межъядерную ось (Λ = 0, 1, 2, … для состояний
, , , ...
);
0,
— символ Кро-
некера,
0,
= 1, если Λ = 0,
0,
= 0 для других значений Λ;
( ),
( )
v
v
r
r
—
колебательные волновые функции возбужденного и основного электронных
состояний.
Радиационное время жизни возбужденного электронно-колебательного
уровня
,
v
с, связано с коэффициентами Эйнштейна соотношением
1
.
v
v v
v
A
(6)
Факторы Франка — Кондона характеризуют относительное распределение
интенсивностей электронно-колебательных полос и представляют собой квад-
раты интеграла перекрывания колебательных волновых функций комбиниру-
ющих электронных состояний
















