Выполняя преобразования этих уравнений, получаем
πD dz q
z
+
πDδ
т
dσ
= 0;
dσ
dz
=
−
q
z
δ
т
.
(1)
Известно, что
σ
=
Eε
=
E
dw
dz
,
(2)
где
E
— модуль упругости;
ε
— относительная деформация.
Подставляя соотношение (2) в (1), получаем дифференциальное уравне-
ние трубопровода при продольном сдвиге грунта:
d
2
w
dz
2
=
−
q
z
Eδ
т
.
(3)
Решение уравнения (3) зависит от вида функции
q
z
(
z
)
, которая описывает
распределение сил сцепления между грунтом и трубопроводом, возникаю-
щих из-за продольного сдвига грунта относительно трубы. Характер этих
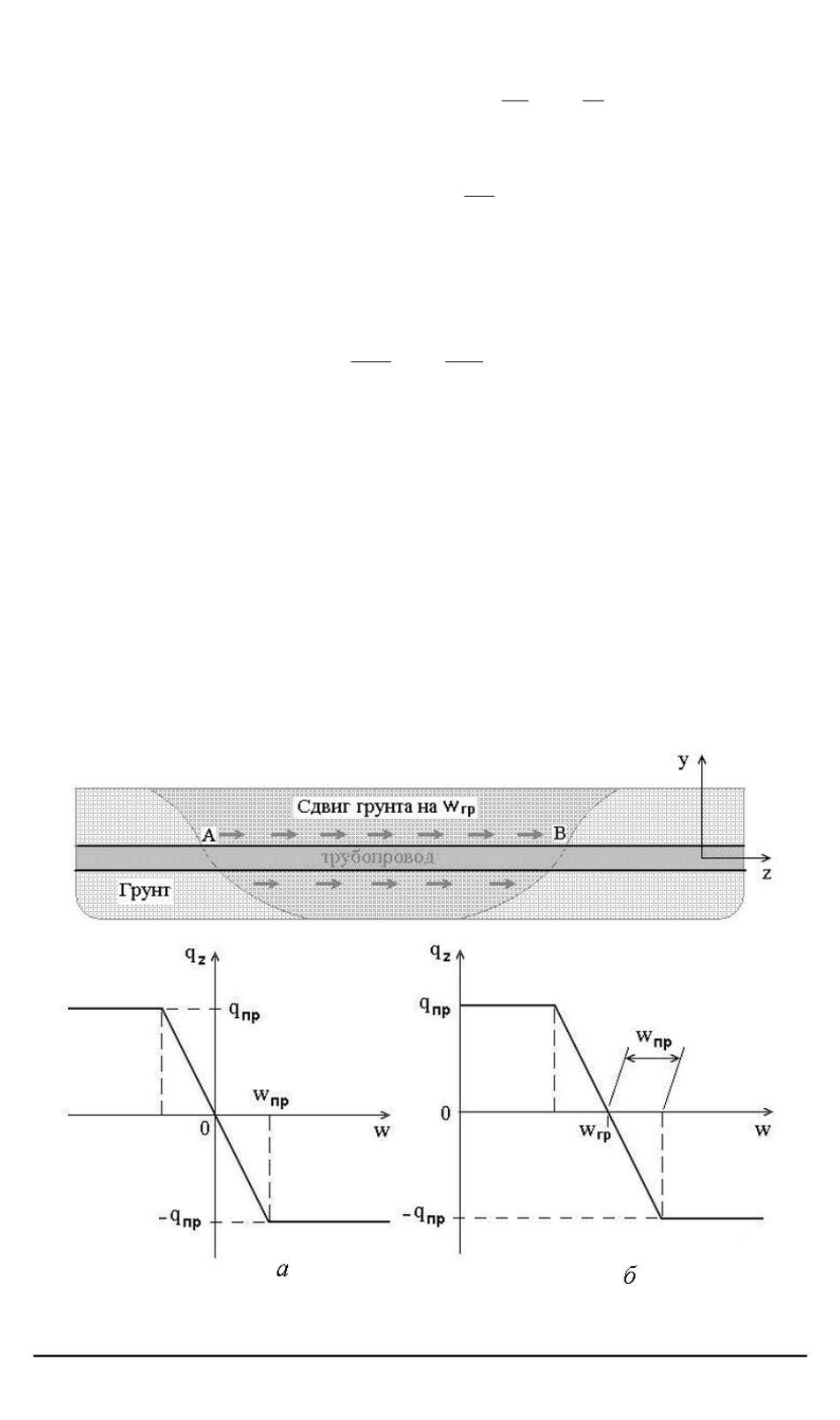
сил показан на рис. 3.
Природа сил сцепления (реакции грунта)
q
z
(
z
)
подобна природе сил
трения. Они растут с увеличением давления грунта снаружи трубы
Р
гр
и
сдвига трубы относительно грунта. Но этот рост может происходить только
до определенного предела, после которого при дальнейшем сдвиге грун-
та реакция остается на достигнутом предельном уровне
q
пр
[2]. Обозначив
смещение трубы через
w
, сдвиг грунта —
w
гр
, относительный сдвиг полу-
чим как разность
(
w
−
w
гр
)
. Давление грунта различно на разных глубинах,
поэтому выберем среднее давление, соответствующее глубине оси трубы:
Рис. 3. Расчетная схема и модели реакции грунта при продольном сдвиге:
а
— за пределами участка
АВ
;
б
— в пределах участка
АВ
112
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 4


