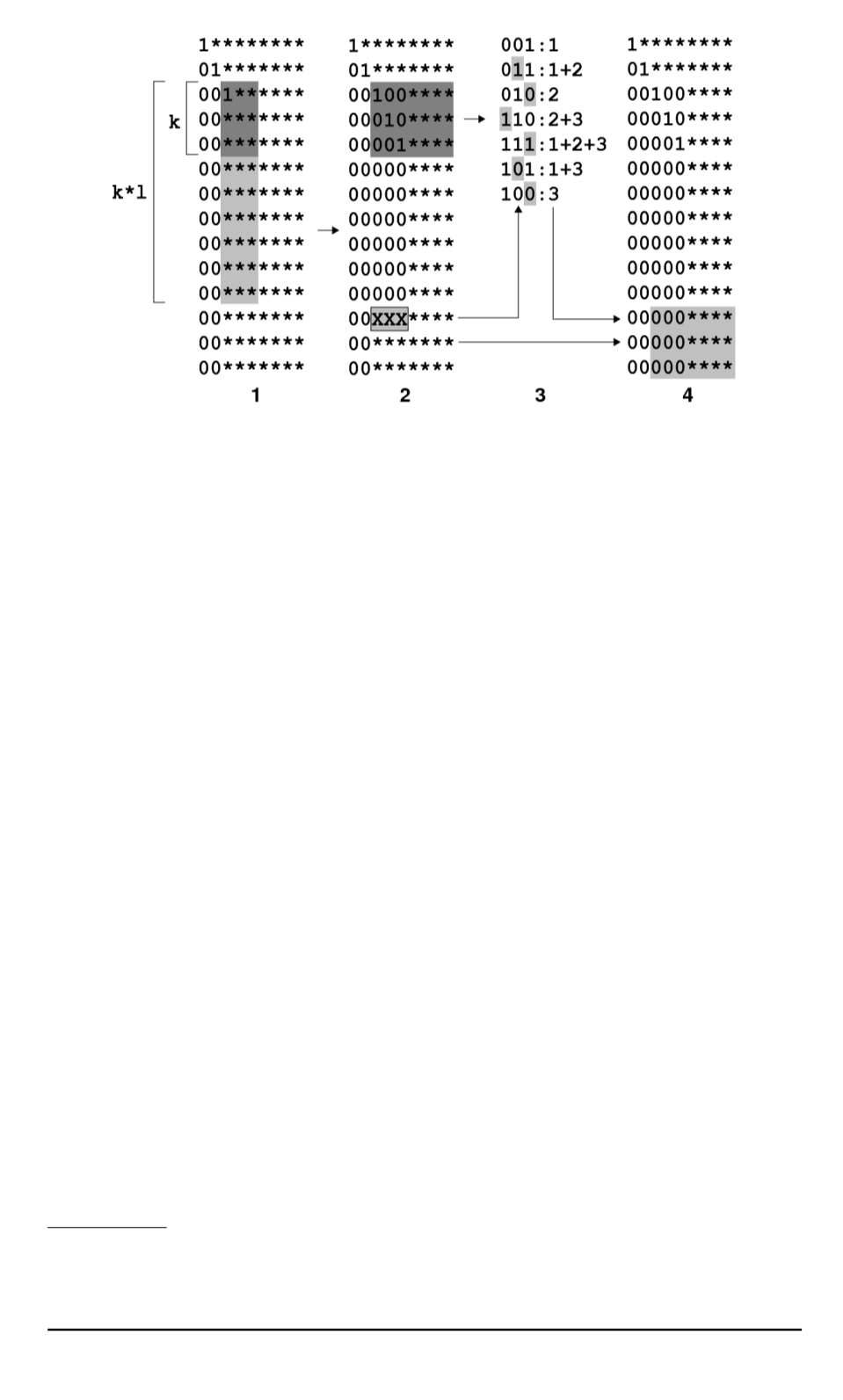
Рис. 1. Метод “четырех русских”
приведения подматрицы к каноническому виду для матрицы с рав-
новероятным распределением нулевых и единичных элементов есть
1
−
m
−
2
.
В [6] показано, что несколько более эффективным является об-
работка подматрицы из
l
∙
k
строк на ЦП, даже с учетом потерь на
пересылку данных в оперативную память и обратно. Это утверждение
было проверено и в авторской реализации. В первом варианте исполь-
зовалось копирование подматрицы в оперативную память и обработка
ее простой реализацией метода Гаусса на ЦП. Область адресного про-
странства, используемая для хранения подматрицы, была зафиксиро-
вана в оперативной памяти и зарегистрирована как таковая в CUDA.
Во втором варианте использовалось единое ядро, содержащее оба ша-
га метода Гаусса. Это удалось сделать за счет того, что рабочая область
памяти невелика и имеет фиксированный размер в течение всего вре-
мени выполнения этого шага. Для кэширования текущей вычитаемой
строки использовалась общая память, поскольку это единственный
вид памяти, доступный из ядра на запись
1
. Получено, что реализация
с обработкой подматрицы на ЦП оказалась более быстрой и в этой
работе. Ускорение невелико и составляет около 3–5% для больших
матриц, но для матриц порядка до
2
13
может достигать 30%.
Данная реализация автоматически уменьшает эффективное
k
при
отсутствии возможности формирования единичной матрицы полного
размера. Поддержка групп столбцов, находящихся в двух смежных
32-битных словах, позволяет получить максимальный прирост произ-
водительности при
k
, не делящих 32 нацело. Тем не менее, алгоритм
1
Не считая глобальной памяти и требующих CUDA capability 2.0 или выше за-
писываемых поверхностей, которые автором не рассматривались из-за ограничений
на их размер.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1
55


