выбором значения
k
и
PLUQ
-разложение
2
(pluq). Для авторской ре-
ализации M4RI на CUDA получены результаты для
k
= 1
(метода
Гаусса),
k
= 4
,
8
и
14
. Результаты для квадратных матриц различного
порядка приведены в таблице. Для исследования влияния производи-
тельности видеокарты на работу алгоритма также использованы дан-
ные, полученные на видеокарте GeForce GTX 550 на машине с ОС
Windows.
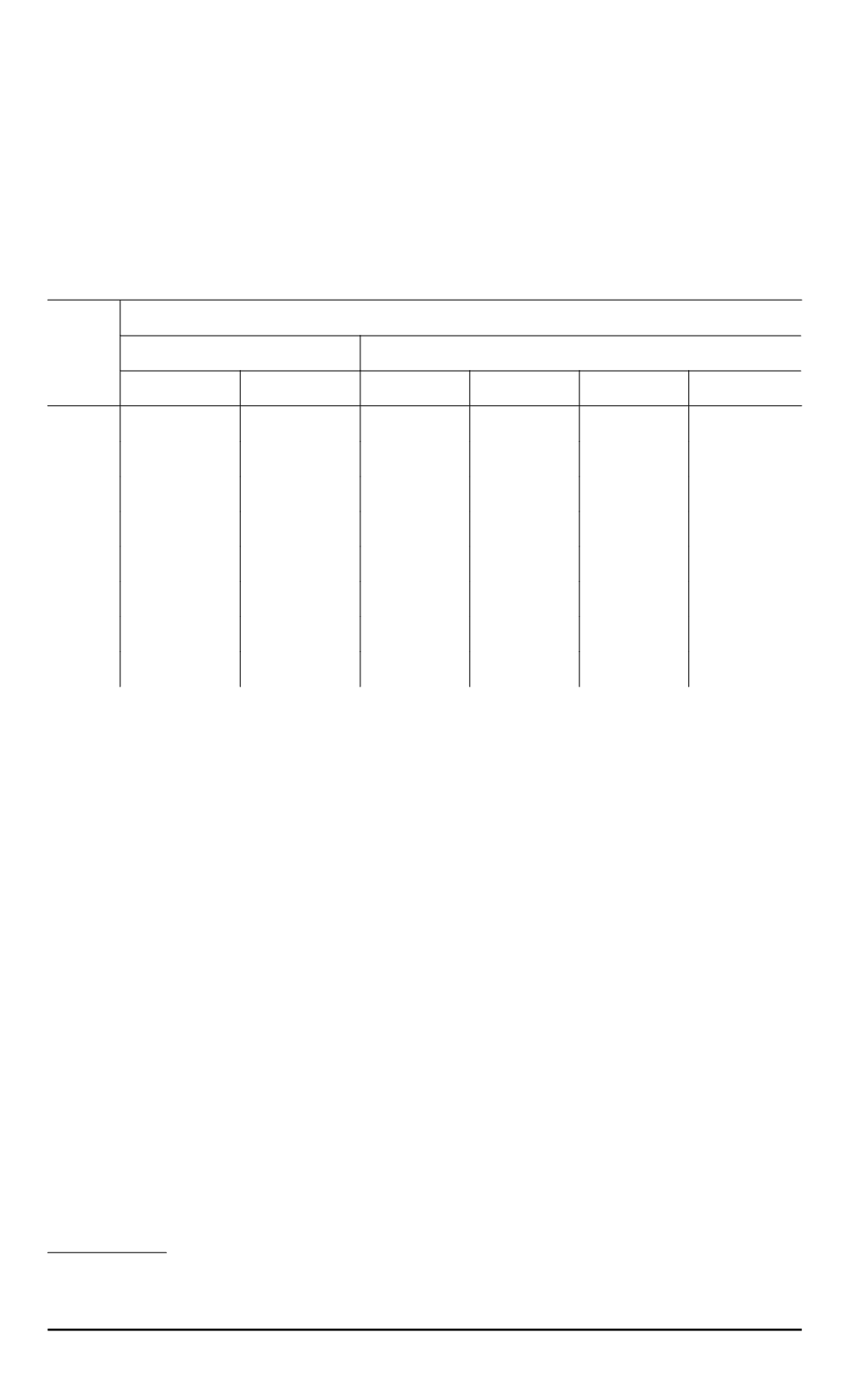
Затраты времени на обработку матриц размера
2
N
×
2
N
Время, с
N
M4RI
CUDA
m4ri
pluq
Гаусс
k
= 4
k
= 8
k
= 14
10
0,00223
0,00254
0,0251 0,0138
0,0107
0,0576
11
0,00601
0,0109
0,0506 0,0262
0,0175
0,115
12
0,0212
0,0525
0,126
0,0604
0,0399
0,238
13
0,113
0,279
0,397
0,182
0,119
0,571
14
1
1,81
1,77
0,797
0,537
1,83
15
7,71
12,5
11
4,89
3,39
4,6
16
85,7
115
77,4
35,1
25,9
20,7
17
1097
928
611
286
209
138
При малых размерах матриц реализация M4RI обладает значи-
тельно меньшей латентностью, поскольку содержит соответствующие
оптимизации, а показатели CUDA включают в себя время на пересыл-
ку матрицы на ГП и обратно и другие постоянные издержки использо-
вания графического адаптера. Для матриц, начиная с размера
2
14
×
2
14
,
вперед выходит реализация на CUDA, причем б ´ольшие
k
показывают
себя лучше на б´ольших матрицах (рис. 3).
Данные результаты в целом соотносятся с ожидаемыми в соот-
ветствии с асимптотической сложностью используемых алгоритмов:
O
(
n
3
)
для метода Гаусса и
O
(
n
3
/
log
n
)
для метода “четырех русских”.
Результаты для метода Гаусса несколько лучше ожидаемых для боль-
шинства матриц, кроме самых малых и самых больших. Это объясня-
ется наличием резерва вычислительной мощности, не используемого
в первом случае и полностью используемого в последнем, данный эф-
фект наблюдается только на самых мощных видеокартах. Для метода
“четырех русских” результаты соответствуют ожидаемым с минималь-
ной погрешностью.
2
Данные методы выбраны как документированные в соответствующем заголо-
вочном файле библиотеки, детально их реализация не рассматривалась.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1
57


