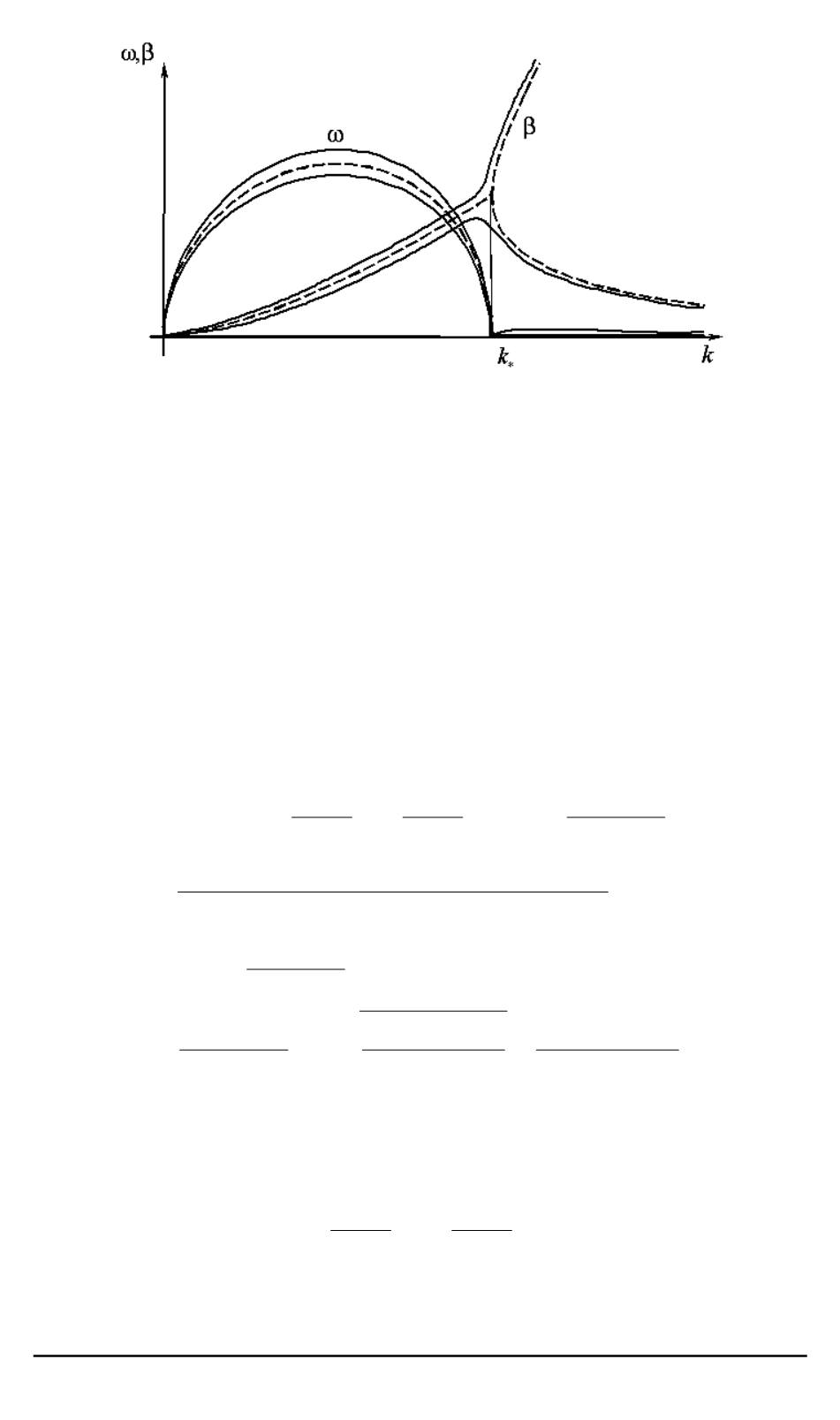
Рис. 1. Схема расщепления колебательной моды и вид решения дисперсионного
уравнения вблизи точки бифуркации (штриховая линия соответствует случаю
θ
= 0)
Образуется своего рода “тонкая структура” периодического затухаю-
щего решения дисперсионного уравнения. Математически это связано
с тем, что уравнение 4-й степени с действительными коэффициентами
может иметь две пары комплексно-сопряженных корней, а аналогич-
ное уравнение с комплексными коэффициентами не приводится к паре
квадратных уравнений с действительными коэффициентами.
Параметрическое представление дисперсионного уравнения.
В случае, когда
U
= 0
, дисперсионное соотношение (1) можно пред-
ставить в параметрическом виде:
˜
ω
2
= 4
u u
3
+
1
−
α
1 +
α
u
−
1
1 +
α
,
˜
β
=
2
u
−
1
(1 +
α
)
u
,
Ω =
4 (1 +
α
)
2
u
6
+ 4 (1
−
α
2
)
u
4
−
4
αu
2
−
1
(1 +
α
)
u
2
, u
>
u
;
(6)
˜
ω
= 0
,
˜
β
=
2
u
−
1
(1 +
α
)
u
;
Ω =
−
1 + 4
αu
2
(1 +
α
)
u
2
+ 4
s
1
−
(1
−
α
)
u
(1 +
α
)
u
,
1
−
(1
−
α
)
u
u
>
0
,
(7)
где
˜
ω
=
Re
(
ω
/
νk
2
)
,
˜
β
=
Im
(
ω
/
νk
2
)
— безразмерные циклическая
частота и коэффициент затухания;
u
— действительный корень урав-
нения
u
3
+
1
−
α
1 +
α
u
−
1
1 +
α
= 0
,
(8)
которое, как нетрудно видеть, совпадает с (4) и определяет положение
точки бифуркации решения.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 3
31


