Бифуркационный анализ для различных спектров волн.
За-
висимости бифуркационных значений параметров
Ω
,
β
,
u
от
α
,
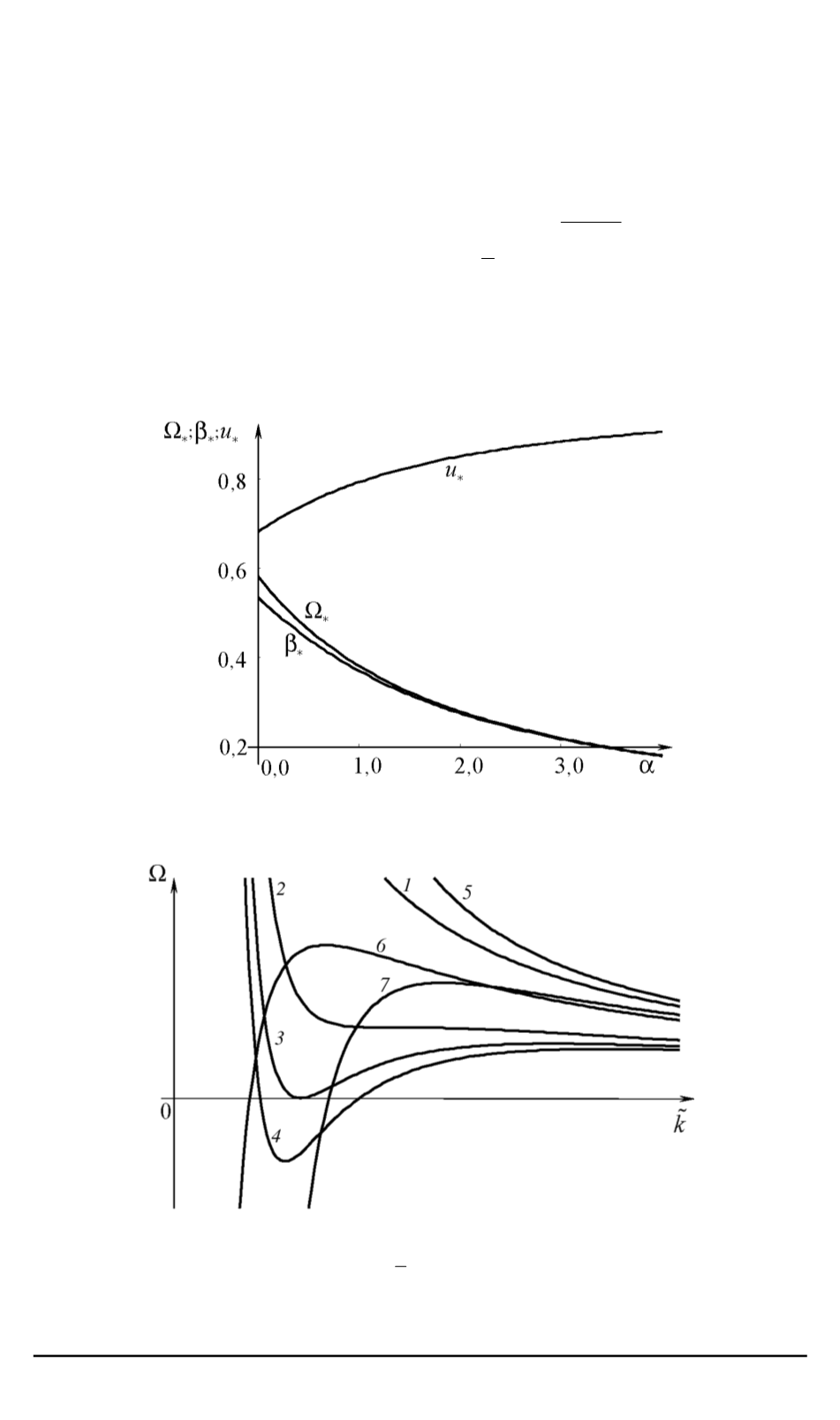
рассчитанные согласно (6)–(7), приведены на рис. 3. При
α
= 1
β
= 1
−
2
−
2/3
≈
0
,
37
,
Ω = 3
−
2
4/3
2
1/3
≈
0
,
3811
, в то время
как при
α
= 0
имеем
Ω
≈
0
,
5814
,
β
≈
0
,
5344
. Из соотношений (9)
следует критическое значение параметра поля, при котором наступа-
ет неустойчивость Френкеля–Тонкса,
F
c
= 2
√
1
−
α
; точка перегиба
функции
Ω ˜
k
появляется при
F
=
F
c
√
3 2
. Вид зависимостей
Ω ˜
k
для различных спектров волн приведен на рис. 4. Зависимости
Ω (
β
)
и
Ω (
k
)
, изображенные на рис. 2 и 4, позволяют качественно описать
характер зависимости
β
(
k
)
.
Рис. 3. Зависимости параметров
Ω
,
β
,
u
от
α
Рис. 4. Зависимости
Ω ˜
k
:
1
—
α <
1
,
F
= 0
;
2
–
α <
1
,
F
=
F
c
√
3
/
2
;
3
—
α <
1
,
F
=
F
c
;
4
—
α <
1
,
F > F
c
;
5
—
α
= 1
,
F
= 0
;
6
—
α
= 1
,
F
6
= 0
;
7
—
α >
1
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 3
33


