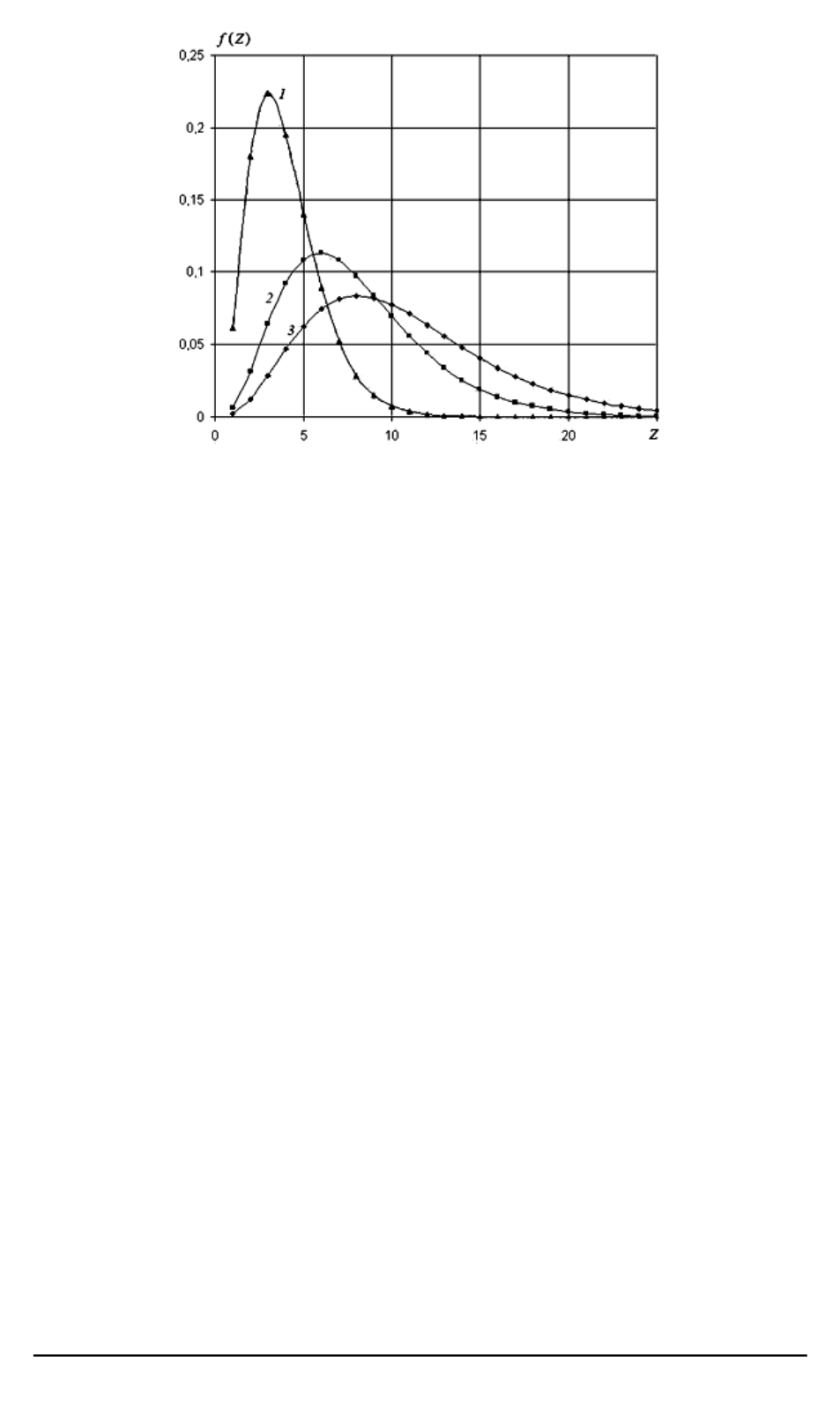
Распределение кластеров по числу содержащихся в них частиц для криптона
на линии насыщения:
1
—
λ
= 0
,
373
,
T
= 117
K;
2
—
λ
= 0
,
505
,
T
= 183
K;
3
—
λ
= 1
,
T
=
T
c
На рисунке приведен общий вид функций распределения кластеров
по числу содержащихся в них частиц
f
(
Z
)
при различных значениях
параметра масштаба
λ
для жидкого криптона. В простых жидкостях
λ
меняется от 0,3 (кристалл вблизи точки плавления) до 1 (в критиче-
ской точке). Причем каждое значение
λ
соответствует определенным
параметрам состояния вещества. Наиболее вероятное значение числа
частиц в кластере соответствует максимуму функции
f
(
Z
)
и может
быть определено для любых значений плотности и температуры. Бо-
лее того, можно оценить максимальное число частиц в кластере, если
связать его с некоторым предельным значением функции
f
(
Z
) = 0
,
01
.
Вблизи точки плавления возможно существование кластеров с числом
частиц 20. . . 22, в критической области максимальное число частиц в
кластере не превышает 10.
В табл. 1 приведены результаты расчетов среднего (
ˉ
Z
) и наибо-
лее вероятного (
ˆ
Z
) значения числа частиц в кластере и их сравнение
с экспериментальными данными для числа
Z
1
ближайших соседей,
полученными на основе анализа радиальной функции распределения
g
(
r
)
. Наблюдается качественное согласие между результатами расче-
тов по распределению Эрланга (7) и определением значений
ˉ
Z
,
ˆ
Z
,
Z
1
рентгеноструктурными методами. Более того, значения первого ко-
ординационного числа
Z
1
лежат между значениями среднего числа
частиц в кластере
ˉ
Z
и наиболее вероятного —
ˆ
Z
(
ˆ
Z
6
Z
1
6
ˉ
Z
). Необ-
ходимо отметить, что погрешность экспериментального определения
величины
Z
1
может достигать 20%. Однако различие между
ˉ
Z
и
ˆ
Z
для
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2
19


