распределения Эрланга превышает 30% (так как
ˉ
Z
= 1
,
33 ˆ
Z
)
, поэтому
отмеченная закономерность имеет место.
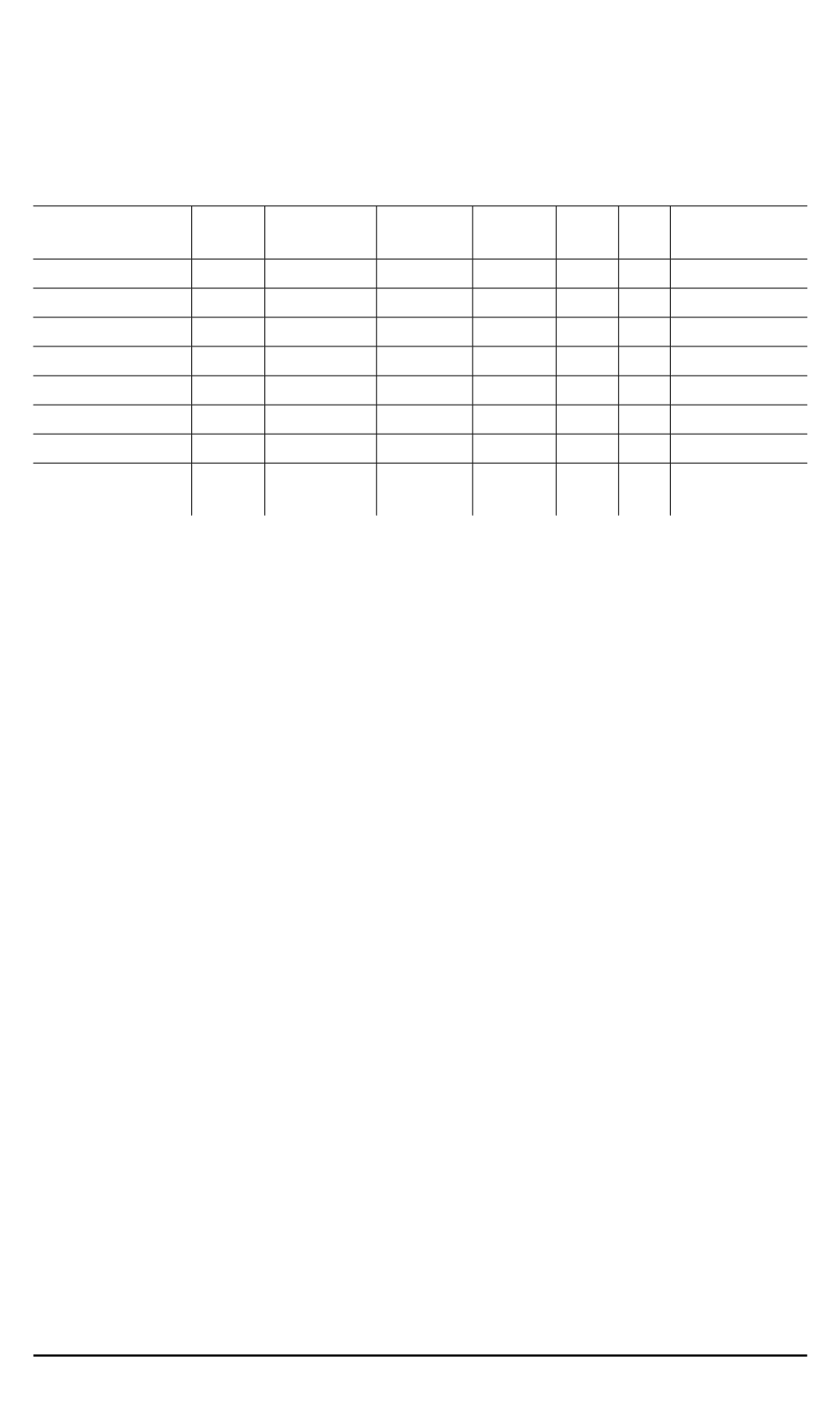
Таблица 1
Среднее (
ˉ
Z
) и наиболее вероятное (
ˆ
Z
) число частиц в кластере для простых
и органических жидкостей
Жидкость
Т
, К
ρ
кр
, кг/м
3
ρ
, кг/м
3
λ
ˉ
Z
ˆ
Z Z
1
(рентген)
[1, 6]
Неон
25
483,0
1240 0,3895 10,3 7,7 8,5
Аргон
85
536,0
1407 0,3809 10,5 7,9 8,9;
10
±
2
Криптон
117 911,0
2442 0,3730 10,7 8,1 8,5
Ксенон
165
1110
2956 0,3755 10,6 8,0 10,0
Азот
77,35 304,0
807,1 0,3770 10,6 8,0 11,8; 9,0
Кислород
90
406,0
1137 0,3571 11,2 8,4 10,4
Толуол
293 290,0
866,9 0,3350 11,9 9,0 11,4
Гексан (нор-
мальный)
293 234,0
659,4 0,3551 11,3 8,5 6. . . 8
Предложенная методика оценки числа частиц в кластере
Z
позво-
ляет установить зависимость этой величины от параметров состояния
вещества (температуры
Т
и давления
Р
), так как параметр масштаба
λ
в распределении Эрланга зависит от плотности вещества
ρ
=
ρ
(
Т
,
Р
)
согласно соотношению (6). Наиболее надежны данные нейтроногра-
фических исследований зависимости первого координационного чи-
сла от температуры
Z
1
=
Z
1
(
T
)
для жидкого криптона вдоль линии
насыщения [1, 6].
В табл. 2 приведены результаты исследования зависимости сред-
него (
ˉ
Z
) и наиболее вероятного (
ˆ
Z
) числа частиц в кластере в функ-
ции температуры для криптона вдоль линии равновесия жидкость–пар
и сравнение с экспериментальными данными для первого координа-
ционного числа
Z
1
[1, 6]. В пределах погрешностей эксперимента
наиболее вероятное число частиц в кластере
ˆ
Z
совпадает с первым
координационным числом
Z
1
для сжиженного криптона.
Эволюция кластера, которая заключается в изменении конфигу-
рации составляющих его частиц (атомов или молекул), теоретически
может быть описана как перемещение точки вдоль поверхности по-
тенциальной энергии кластера в многомерном пространстве координат
атомов [5, 8].
В рамках наших предположений ядро кластера — димер, вокруг
которого формируется первая координационная сфера с числом частиц
ˉ
Z
1
= ˉ
Z
−
2
.
(10)
Поверхность координационной сферы можно считать поверхно-
стью потенциальной энергии кластера, значение которой определяется
20
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2


