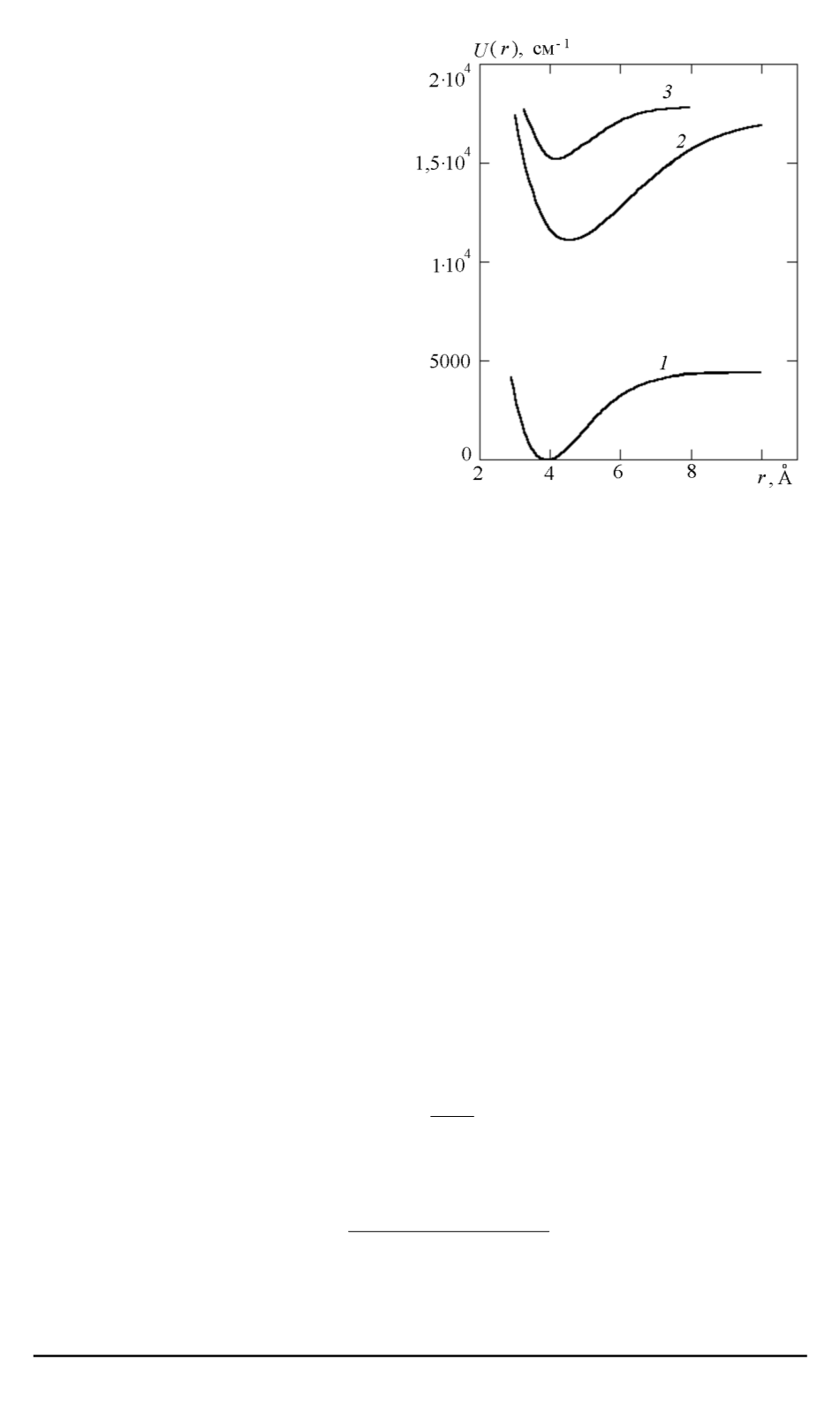
Рис. 1. Потенциальные кривые для
основного
X
1
Σ
+
g
(1) и возбужденных
A
1
Σ
+
u
(2),
B
1
Π
u
(3) электронных состо-
яний молекулы
39
K
2
основе построенных потенци-
альных кривых. Расчет враща-
тельных и центробежных по-
стоянных проведен по теории
возмущений для модели враща-
ющегося осциллятора двухатом-
ной молекулы [11]. В табл. 3
приведены результаты сравне-
ния рассчитанных колебатель-
ных энергий и вращательных
молекулярных постоянных с
экспериментальными величина-
ми. На рис. 2 и 3 приведе-
ны результаты расчета центро-
бежных постоянных. Рассчитан-
ные на основе полуэмпири-
ческих потенциальных кривых
колебательные энергии, враща-
тельные и центробежные посто-
янные аппроксимированы сте-
пенными функциями, параметры которых являются молекулярными
постоянными
E
v
=
ω
e
(
v
+ 0
,
5)
−
ω
e
x
e
(
v
+ 0
,
5)
2
+
. . . ,
(3)
B
v
=
B
e
−
α
e
(
v
+ 0
,
5) +
γ
e
(
v
+ 0
,
5)
2
+
. . . ,
(4)
D
v
=
D
e
−
β
e
(
v
+ 0
,
5) +
δ
e
(
v
+ 0
,
5)
2
+
,
(5)
H
v
=
H
e
−
ξ
e
(
v
+ 0
,
5) +
e
(
v
+ 0
,
5)
2
+
. . . .
(6)
Полученные из оптимальных аппроксимирующих функций молеку-
лярные постоянные приведены в табл. 4 и сравниваются с эксперимен-
тальными значениями. Для сопоставления с полученными результата-
ми значения центробежных постоянных
D
e
и
H
e
также были рассчи-
таны с использованием экспериментальных колебательных и враща-
тельных постоянных по эмпирическим соотношениям Кратцера [12]
D
e
=
4
B
3
e
ω
2
e
(7)
и Кэмбла и др. [13]
H
e
=
2
D
e
(12
B
2
e
−
α
e
ω
e
)
3
ω
2
e
.
(8)
Рассчитанные по соотношениям (7) и (8) центробежные постоян-
ные приведены в табл. 4.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 2
71


