Математическое моделирование стационарного температурного состояния конструкции методом локальных вариаций - page 3

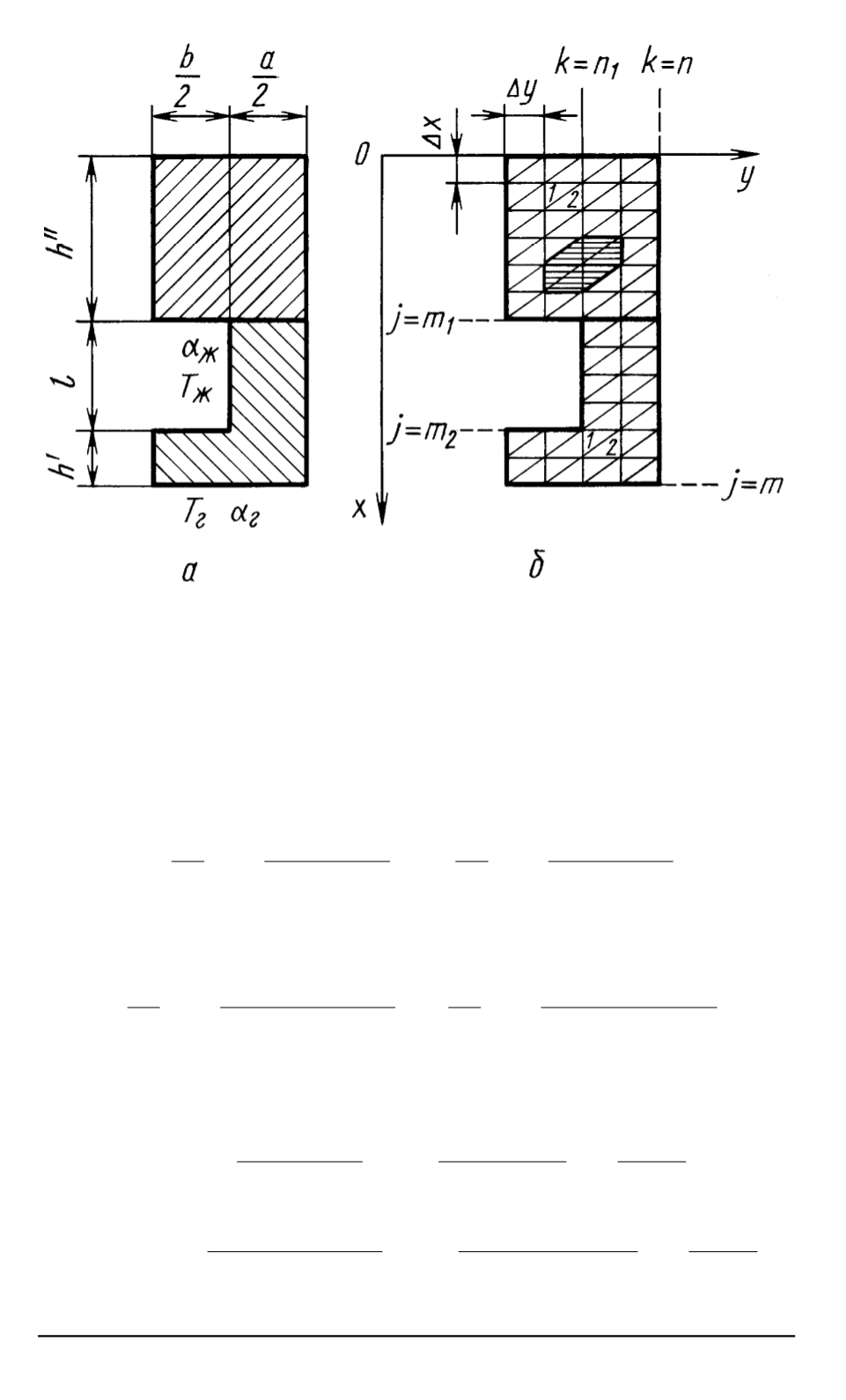
Рис. 1. Повторяющийся элемент оболочки:
а — исходящая область; б — триангуляция области
Mj +1,k, M j,k+1 соответственно. Частные производные в формуле (6)
приближенно представим следующими конечно-разностными форму -
лами: для треугольных ячеек с вершинами Mjk , Mj +1,k , M j,k+1 (ячеек 1
на рис. 1, б ) —
µ ∂T
∂x ¶1
=
Tjk − Tj +1,k
∆x
, µ ∂T
∂y ¶1
=
Tj,k+1 − Tjk
∆y
; (8)
для треугольных ячеек с вершинами M j +1,k+1 , Mj +1,k, Mj,k +1 (ячеек 2 на
рис. 1, б ) —
µ ∂T
∂x ¶2
=
Tj,k +1 − Tj+1,k+1
∆x
, µ ∂T
∂y ¶2
=
Tj +1,k+1 − Tj +1,k
∆y
. (9)
Получим формулы вычисления функционала для ячеек с вершина -
ми во внутренних узлах:
I 1
jk = λjk à µTjk − Tj +1,k
∆x ¶2
+ µ T j,k+1 − Tjk
∆y ¶2 ! ∆x∆y
4
, (10)
I 2
jk = λjk à µTj,k +1 − Tj +1,k+1
∆x ¶2
+ µ T j +1,k+1 − Tj +1,k
∆y ¶2 ! ∆x∆y
4
;
(11)
ISSN 1812-3368. Вестник МГТУ им . Н.Э. Баумана. Сер. “Естественные науки”. 2004. № 3 43