Изменение значения
T
jk
(
x
j
, y
k
)
в одном внутреннем узле сетки вы
-
зывает изменения функционала только в шести слагаемых
,
входящих в
сумму
(7).
Сумму этих слагаемых обозначим выражением
Φ =
I
1
jk
+
I
2
j
−
1
,k
+
I
1
j
−
1
,k
+
I
2
j
−
1
,k
−
1
+
I
1
j,k
−
1
+
I
2
j,k
−
1
.
(16)
При замене
T
jk
на
T
jk
+
h
или
T
jk
−
h
имеем суммы
Φ
+
и
Φ
−
соот
-
ветственно
.
Если при замене
,
например
,
T
jk
на
T
jk
+
h
значение функ
-
ционала
I
окажется меньше соответствующего значения
,
полученно
-
го на предыдущей итерации
,
т
.
е
.
Φ
+
<
Φ
,
то вместо
T
jk
принимаем
новое значение
T
jk
+
h
.
В противном случае заменяем
T
jk
на
T
jk
−
h
и сравниваем
Φ
и
Φ
−
.
В случае
,
если обе замены не уменьшают зна
-
чения суммы
(7),
в памяти ЭВМ сохраняем значение
T
jk
,
полученное
на предыдущей итерации
.
После обхода всех узлов сетки переходим к
следующей итерации
,
которую выполняем аналогичным образом
.
Шаг
варьирования уменьшаем
,
если на очередной итерации температура во
всех узлах осталась неизменной
.
Процесс варьирования температуры
на данной сетке завершаем при выполнении условия
h <
ε
2
,
(17)
где
ε
—
заданное положительное достаточно малое число
.
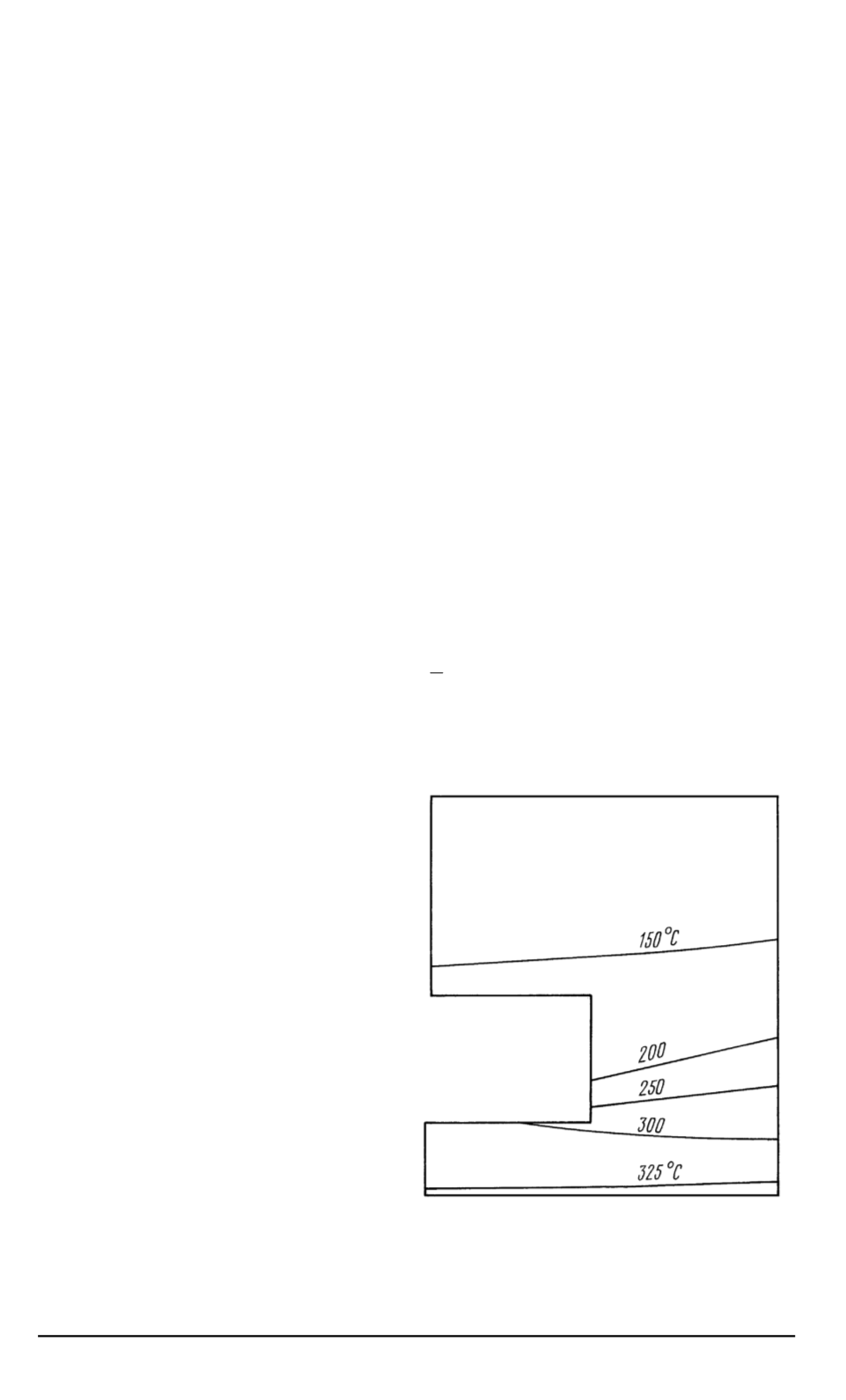
Рис
. 2.
Результаты расчета распределе
-
ния температуры по описанному алго
-
ритму
Затем варьируем температу
-
ру на более мелкой сетке
,
уве
-
личив
m
,
n
(
например
,
вдвое
),
т
.
е
.
уменьшив
∆
x,
∆
y
.
В каче
-
стве исходных данных прини
-
маем значения
,
полученные из
решения на предыдущей сетке
,
причем значения для новых уз
-
лов более мелкой сетки получа
-
ем путем интерполяции
.
Варьи
-
рование реализуется аналогично
рассмотренному выше
.
Результаты расчета распре
-
деления температуры по опи
-
санному алгоритму представле
-
ны на рис
. 2.
Решение получено с
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2004.
№
3
45


