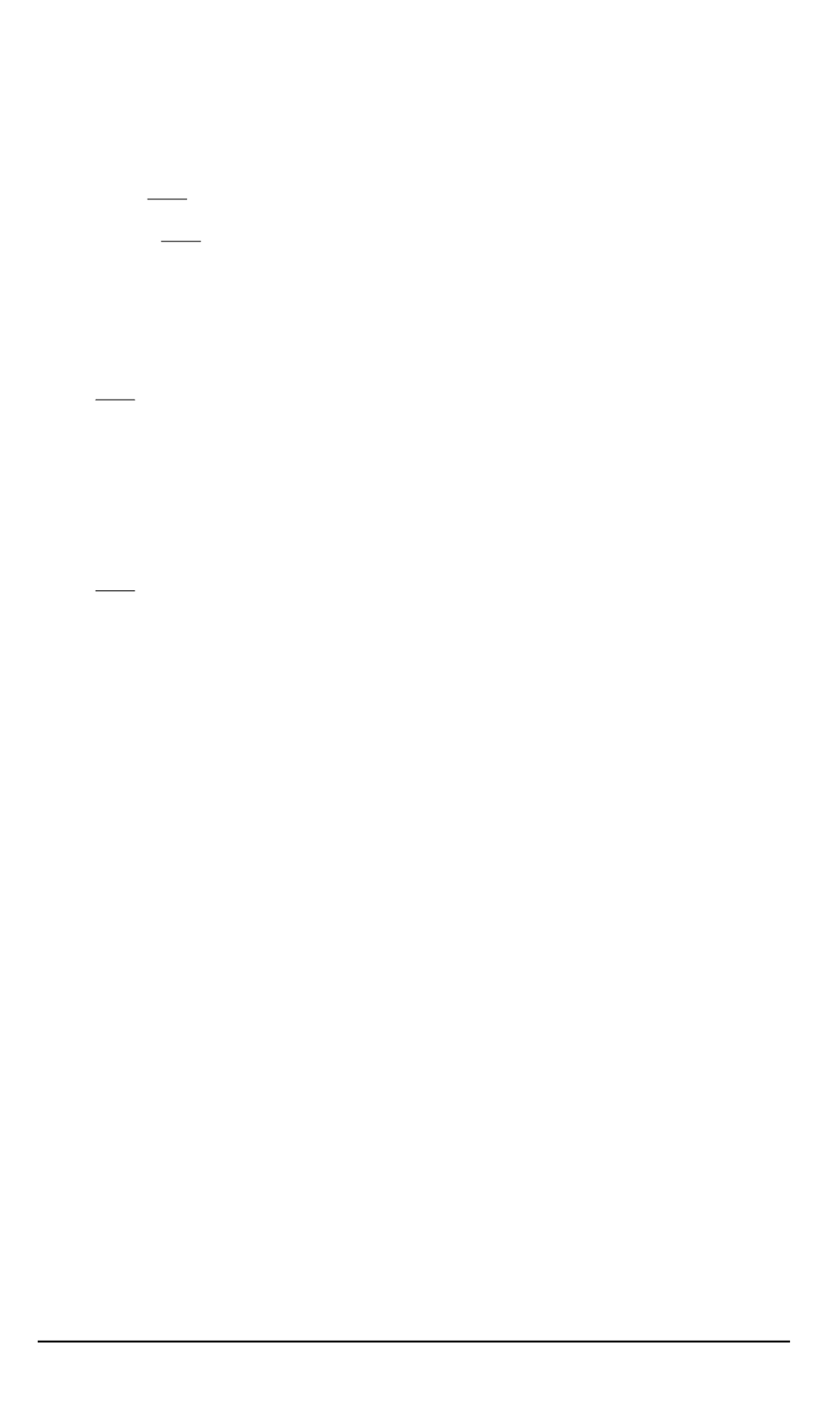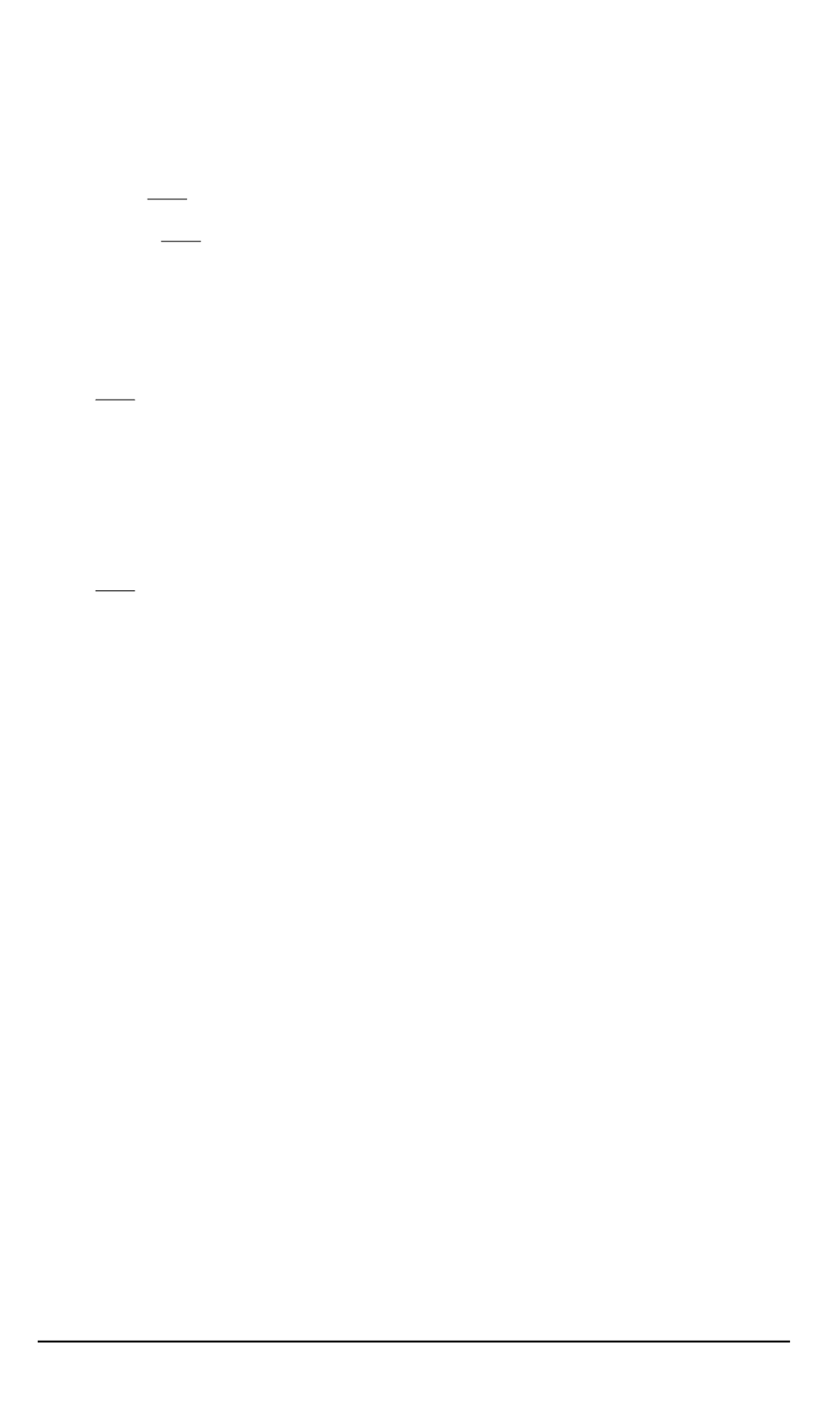
Доказательство теоремы
.
Доказательство проведем по индукции
.
Нетрудно видеть
,
что для
n
= 0
и
n
= 1
утверждение теоремы спра
-
ведливо
,
так как
d
0
= 1
,
f
0
= 0
,
d
1
= 2
L
1
1
(
−
u
) = 2
u
+ 4
,
f
1
=
−
1
.
Предположим
,
что для некоторых
n
−
1
,
n
,
n
∈ {
2
,
3
, ...
}
,
выполнено
m
2
n
−
1
=
p
π/
2
σ
2
n
−
1
e
−
u/
2
(((
u
+1)
d
n
−
1
+
f
n
−
1
)
I
0
(
u/
2) +
ud
n
−
1
I
1
(
u/
2))
,
m
2
n
+1
=
p
π/
2
σ
2
n
+1
e
−
u/
2
(((
u
+ 1)
d
n
+
f
n
)
I
0
(
u/
2) +
ud
n
I
1
(
u/
2))
.
Подставив последние выражения в равенство
(2),
получим
m
2
n
+3
=
=
p
π/
2
σ
2
n
+3
e
−
u/
2
³³
2(2
n
+ 2 +
u
)
d
n
−
(2
n
+ 1)
2
d
n
−
1
´
(
u
+ 1)+
+
³
2(2
n
+ 2 +
u
)
f
n
−
(2
n
+ 1)
2
f
n
−
1
)
´
I
0
(
u/
2)+
+
³
2(2
n
+ 2 +
u
)
d
n
−
(2
n
+ 1)
2
d
n
−
1
´
uI
1
(
u/
2)
´
=
=
p
π/
2
σ
2
n
+3
e
−
u/
2
(((
u
+ 1)
d
n
+1
+
f
n
+1
)
I
0
(
u/
2) +
ud
n
+1
I
1
(
u/
2))
.
Теорема доказана
.
Далее приведены первые шесть коэффициентов
d
n
и
f
n
:
d
0
=
L
1
0
(
−
u
)
≡
1
,
d
1
= 2
L
1
1
(
−
u
) = 2
u
+ 4
,
d
2
= 8
L
1
2
(
−
u
)
−
L
3
0
(
−
u
) = 4
u
2
+ 24
u
+ 23
,
d
3
= 48
L
1
3
(
−
u
)
−
4
L
3
1
(
−
u
) = 8
u
3
+ 96
u
2
+ 284
u
+ 176
,
d
4
= 384
L
1
4
(
−
u
)
−
24
L
3
2
(
−
u
) + 9
L
5
0
(
−
u
) =
= 16
u
4
+ 320
u
3
+ 1908
u
2
+ 3720
u
+ 1689
,
d
5
= 3840
L
1
5
(
−
u
)
−
192
L
3
3
(
−
u
) + 54
L
5
1
(
−
u
) =
= 32
u
5
+ 960
u
4
+ 9568
u
3
+ 37824
u
2
+ 54774
u
+ 19524
,
f
0
= 0
,
f
1
=
−
L
3
0
(
−
u
)
≡ −
1
,
f
2
=
−
2
L
3
1
(
−
u
) =
−
(2
u
+ 8)
,
f
3
=
−
8
L
3
2
(
−
u
) + 9
L
5
0
(
−
u
) =
−
¡
4
u
2
+ 40
u
+ 71
¢
,
f
4
=
−
48
L
3
3
(
−
u
) + 36
L
5
1
(
−
u
) =
=
−
¡
8
u
3
+ 144
u
2
+ 684
u
+ 744
¢
,
f
5
=
−
384
L
3
4
(
−
u
) + 216
L
5
2
(
−
u
)
−
225
L
7
0
(
−
u
) =
=
−
¡
16
u
4
+ 448
u
3
+ 3924
u
2
+ 11928
u
+9129
¢
.
ISSN 0236-3933.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
1 91