
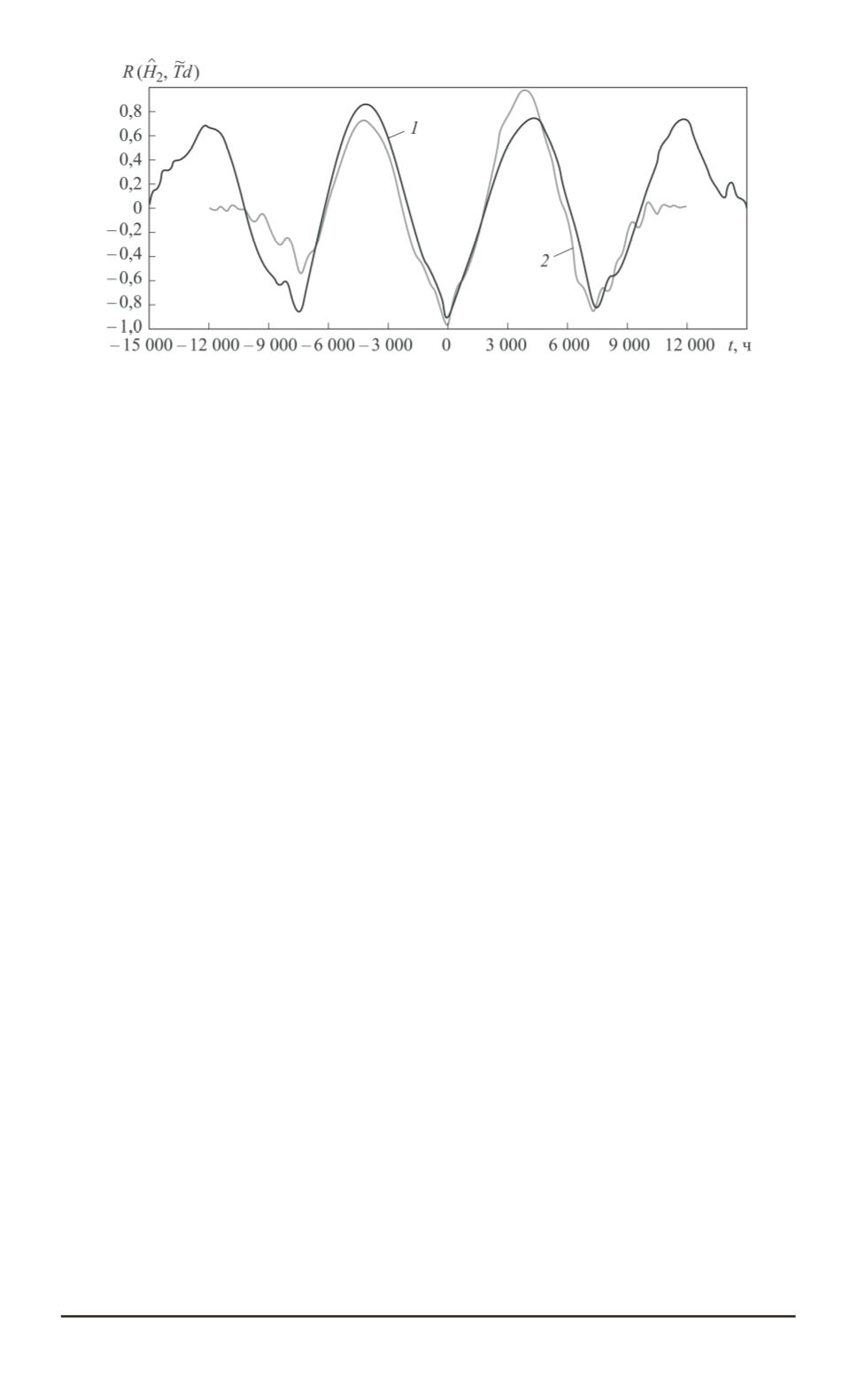
Рис. 1. Корреляционные функции мер Кульбака
ˆ
H
2
и температуры точки росы
˜
T d
для экспериментальной установки № 2 в первой (
1
) и второй (
2
) сериях
экспериментов
Согласно приведенным в табл. 1 данным, для экспериментальной
установки № 1 в первой серии экспериментов вследствие более вы-
сокого уровня шума корреляции не наблюдаются. Во второй серии
экспериментов установка № 1 показывает меньшие значения коэффи-
циентов корреляции, чем установка № 2. Коэффициент корреляции
с атмосферным давлением
P
наблюдается достаточно надежно толь-
ко для установки № 2 в первой серии экспериментов. В двух сериях
экспериментов установка № 2 показывает наибольшие коэффициенты
корреляции.
Наибольшие значения коэффициентов корреляции (
R
ˆ
H
2
,
˜
T d
=
=
−
0
,
906
и
R
ˆ
H
2
,
˜
T d
=
−
0
,
959
для первой и второй серий экспери-
ментов) наблюдаются для установки № 2 при расчете влияния на меру
Кульбака
ˆ
H
2
температуры точки росы
˜
T d
. Корреляционные функции
для экспериментальной установки № 2 в первой (кривая
1
) и второй
(кривая
2
) сериях экспериментов приведены на рис. 1.
Наблюдаемая корреляция проиллюстрирована на рис. 2 зависимо-
стями меры Кульбака
ˆ
H
2
и температуры точки росы
˜
T d
от времени для
первой (рис. 2,
а
) и второй (рис. 2,
б
) серий экспериментов. На приве-
денных кривых хорошо просматривается явная зависимость значений
меры Кульбака
ˆ
H
2
(кривая
1
) от температуры точки росы
˜
T d
(кри-
вая
2
), причем совпадают не только сверхдлиннопериодные процессы,
с повторяемостью порядка одного года, но и более высокочастотные,
которые имеют периоды около 500 ч (около 20 сут.). При этом зависи-
мость меры Кульбака
ˆ
H
2
от температуры точки росы
˜
T d
обратная (см.
температурную ось с правой стороны рис. 2).
Проведем оценку влияния различных метеорологических факторов
на значения мер Кульбака. Рассчитанные значения коэффициентов ре-
60
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 4

















