
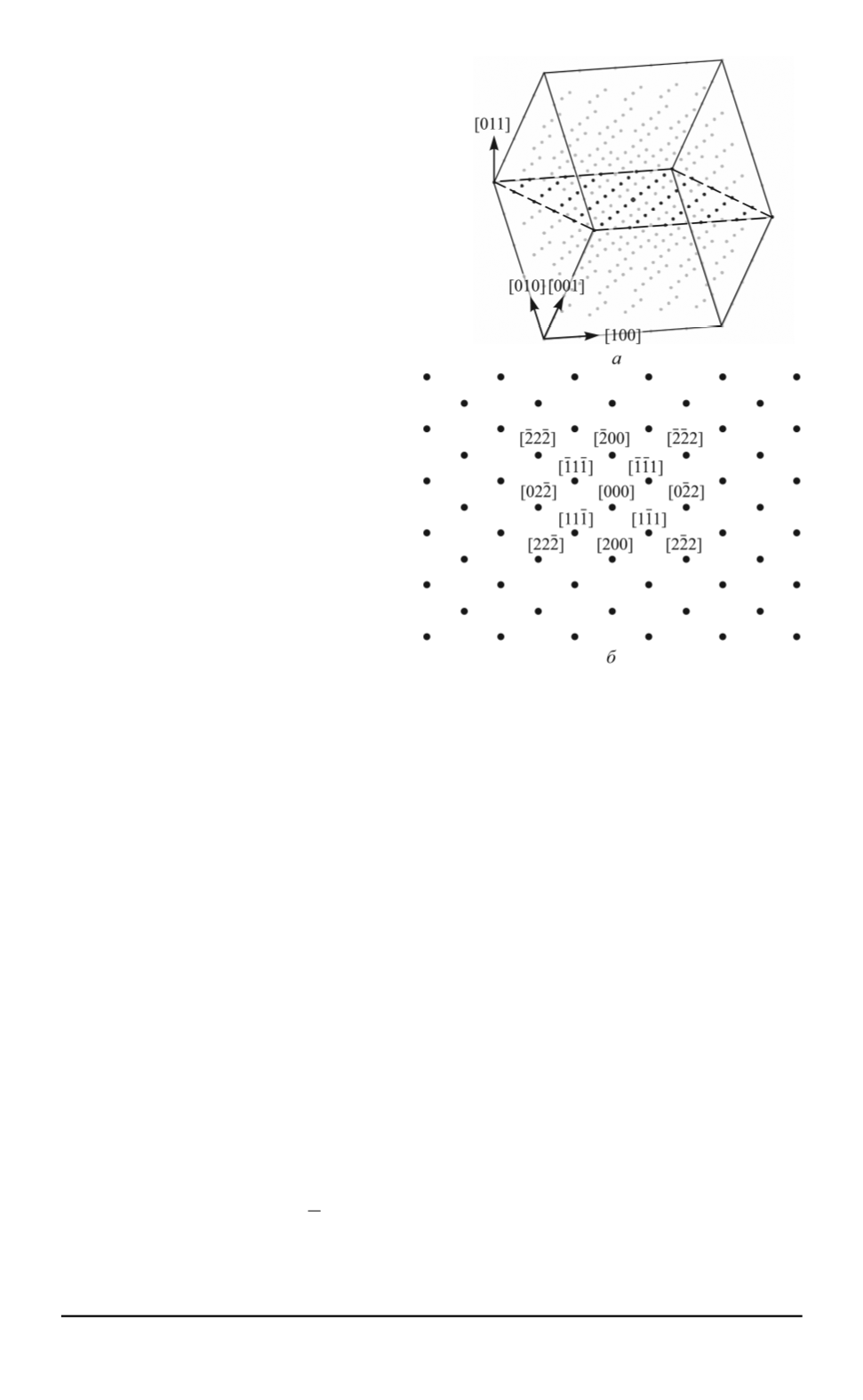
Рис. 1. Модель ГЦК-решетки в обратном
пространстве (
а
) и сечение [011] (
б
)
результатами. В действитель-
ности узлы обратной решетки
не являются точечными. Фор-
ма и распределение интенсив-
ности узла зависит от фор-
мы кристалла (фактор формы)
[10, 11]. Вследствие того, что
узлы обратной решетки вытяну-
ты вдоль нормального направле-
ния плоскости фольги и, сле-
довательно, пересекают сферу
отражения в интервале углов,
существует диапазон отражаю-
щих положений для каждого
узла. Для упрощения модели
дифракции анизотропия формы
узлов была скомпенсирована
“толщиной” сечения обратного
пространства, а с учетом дли-
ны волны электронов и, сле-
довательно, достаточно большо-
го радиуса сферы отражения
относительно параметров кри-
сталлической решетки, кривиз-
ной сферы также можно пренебречь и использовать плоское сече-
ние обратного пространства. Границы диапазона отражающих поло-
жений подбирались экспериментально с учетом близлежащих к точно-
му отражающему положению узлов обратной решетки. Модель ГЦК-
решетки в обратном пространстве и сечение [011] приведены на рис. 1.
Моделирование обратной решетки фазовых включений выполня-
лось с учетом известных ориентационных соотношений фазы и ма-
трицы. При этом учитывались все возможные кристаллографически
эквивалентные ориентации включений. Алгоритм поиска кристалло-
графически эквивалентных ориентаций основан на поочередной пере-
становке индексов всех направлений ориентационного соотношения
с проверкой полученных векторов на компланарность. Полученные
ориентации не должны повторяться. Описанный алгоритм возвращает
все возможные кристаллографически эквивалентные ориентации для
заданного типа ориентации фазы в матричной решетке. Например,
для
S
0
-фазы [12, 13] с ориентационным соотношением
[100]
k
[100]
α
,
[010]
S
k
[012]
α
,
[001]
S
k
[021]
α
число кристаллографически эквивалент-
ных ориентаций составляет 12. Полученные ориентации представле-
ны в таблице. Результаты моделирования решетки
S
0
-фазы в обратном
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 2
37
















