
Для получения вспомогательного изображения применялся фильтр
Ланцоша. Продолжение амплитудного спектра, т.е. его экстраполяция
в область высоких частот, осуществляется с помощью разрезов спек-
тра.
Разрезом
s
(
k
)
амплитудного спектра
A
(
m, n
)
,
m, n
∈
[0;
N
−
1]
, по-
строенным для угла
α
, назовем последовательность чисел
s
(0)
, . . . , s
(
N
−
1)
,
s
(
k
) = ˜
A
(
k
cos
α, k
sin
α
)
. Значения разреза в точках
с нецелыми координатами вычисляются интерполяцией (2). Строится
набор разрезов для углов
α
∈
[0;
π
)
, в силу симметрии амплитудного
спектра значения разреза при
α
∈
[
π
; 2
π
)
не рассчитываются. Число
разрезов
S
задается равным разрешению результирующего изобра-
жения. Таким образом, период углов, с которым получаются разрезы
матрицы амплитудного спектра, равен
Δ
α
≈
arctg (1
/
(
qN
))
, где
q
—
коэффициент масштабирования;
N
— размер исходного изображе-
ния. Каждый разрез, состоящий из
N
чисел, пополняется до числа
pN
путем экстраполяции. Для экстраполяции применяется не весь
разрез, а только некоторая его часть при значениях
k
от
N
0
до
N
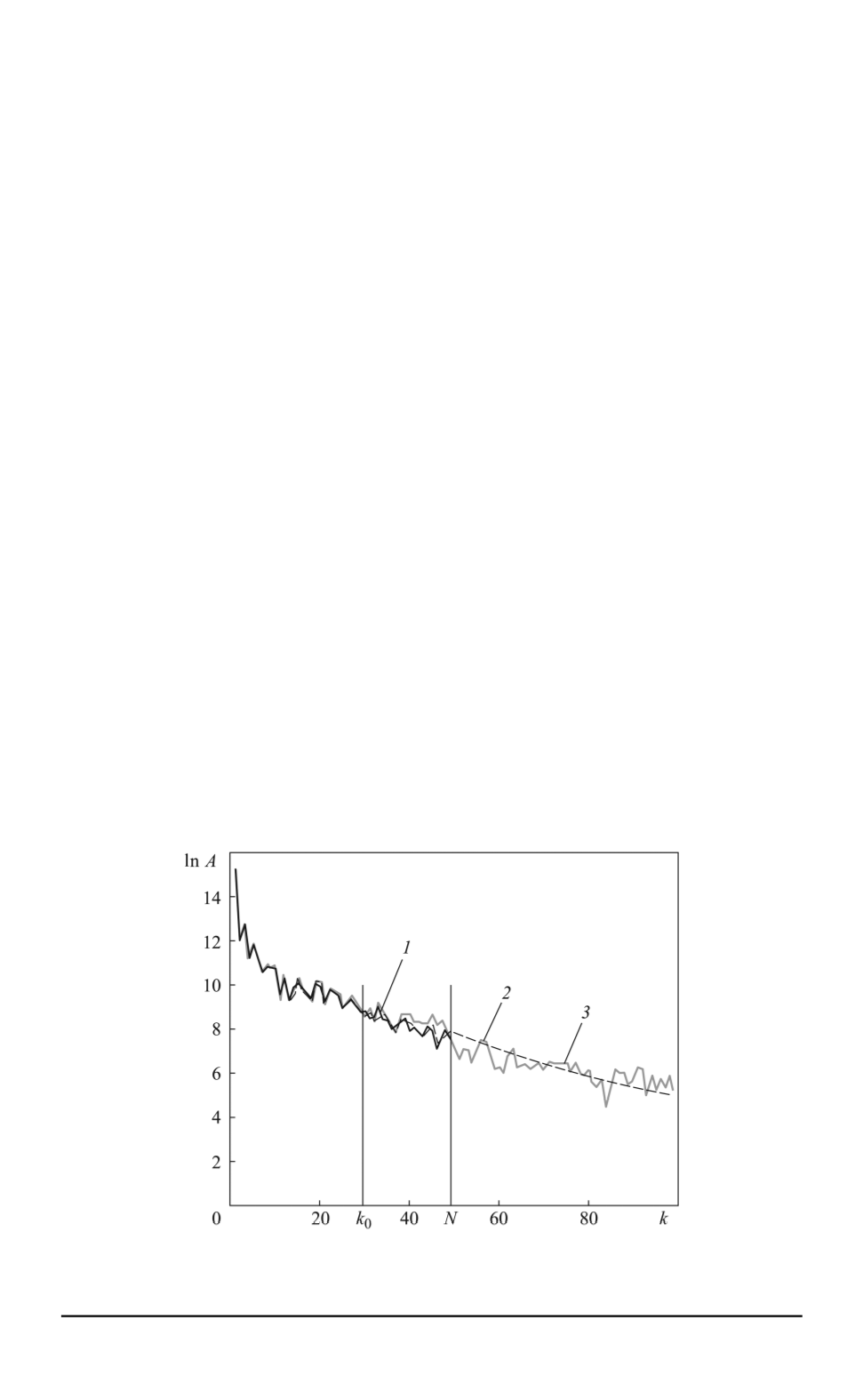
(рис. 2). Зависимость амплитудного спектра пространственных волн
от волнового числа
k
может быть описана степенной функцией с
показателем степени
p
. С учетом этого все разрезы линеаризуются
путем логарифмирования. Получается линейная зависимость с неко-
торым углом наклона
tg
p
, которая продолжается в область высоких
частот. Затем проводится экспоненциирование и получается набор из
разрезов, имеющих продолжение в область высоких частот. На сле-
дующем этапе совершается обратный переход от набора разрезов к
амплитудному спектру изображения. Для этого так же, как и на этапе
построения разрезов, вычисляются значения в точках дискретного
Рис. 2. Зависимость амплитудного спектра пространственных волн от волно-
вого числа для исходного (
1
), эталонного (
2
) и продолженного (
3
) спектров
96
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 2
















