
А.И. Богоявленский
6
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 2
Формальная постановка задачи.
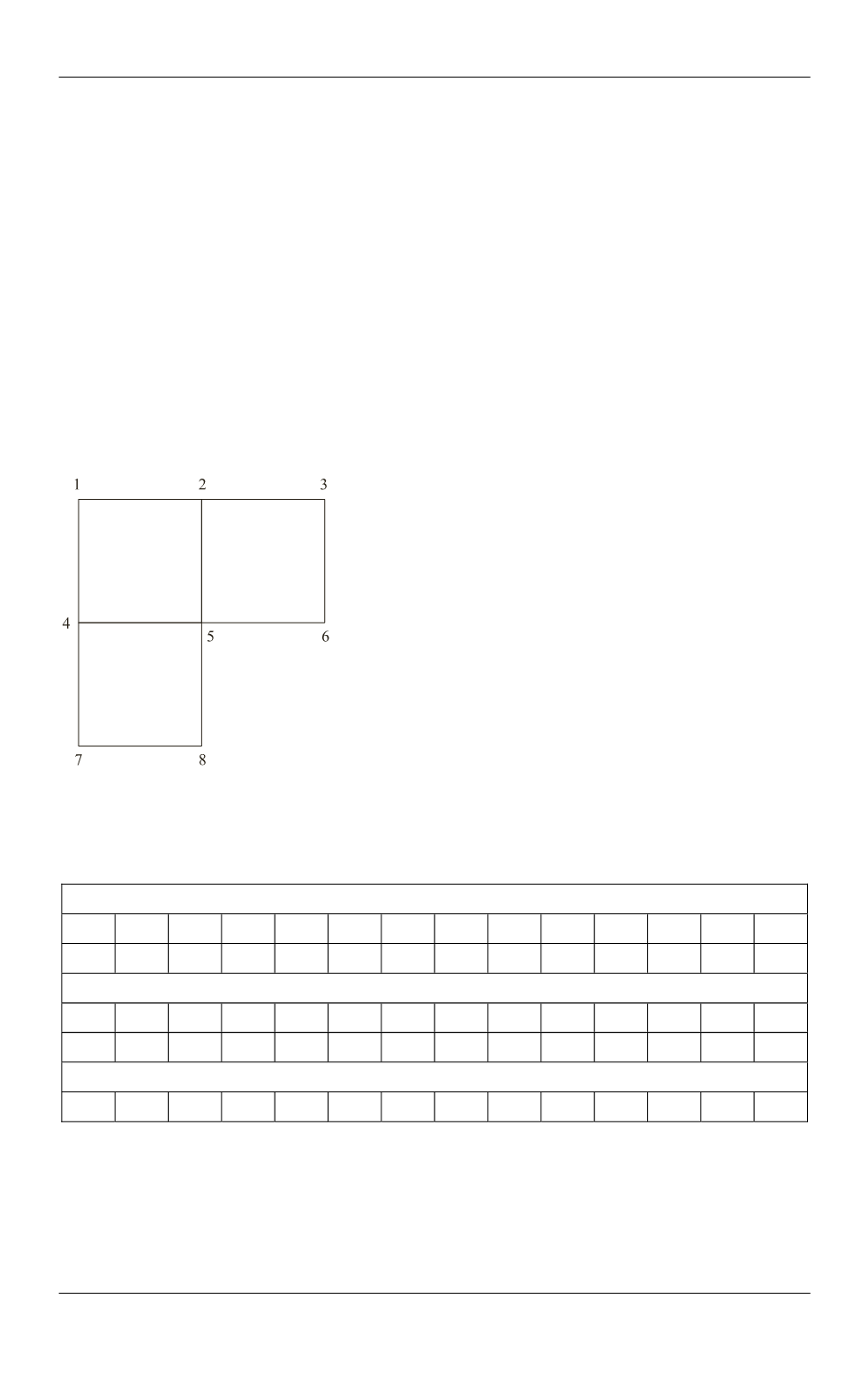
Рассмотрим простую двумерную сетку
(рисунок) и собранную на ее основе матрицу
K
коэффициентов СЛАУ МКЭ в
полной символьной форме:
11 12
14
21 22 23
25
32 33
36
41
44 45
47
52
54 55 56
58
63
65 66
74
77 78
85
87 88
0
0 0 0 0
0
0 0 0
0
0 0
0 0
0 0
0
0
.
0
0
0
0 0
0
0 0
0 0 0
0 0
0 0 0 0
0
k k
k
k k k
k
k k
k
k
k k
k
k
k k k
k
k
k k
k
k k
k
k k
(2)
Структура формата
CCS
состоит из трех
одномерных массивов, которые обозначим как
vals(), row_inds()
и
col_ ptr()
[4]. Массив
vals()
хранит ненулевые коэффициенты матрицы
,
K
массив
row_inds()
— их строчные индексы, для
каждого столбца матрицы массив
col_ ptr()
—
указатель на индекс ненулевого коэффици-
ента массива
vals()
, являющийся последним в
этом столбце. Пример заполненных масси-
вов
CCS
для матрицы (2) приведен в таблице.
Содержимое формата
CCS
для матрицы (2)
vals()
k
11
k
21
k
41
k
12
k
22
k
32
k
52
k
23
k
33
k
63
k
14
k
44
k
54
k
74
k
25
k
45
k
55
k
65
k
85
k
36
k
56
k
66
k
47
k
77
k
87
k
58
k
78
k
88
row_inds()
1
2
4
1
2
3
5
2
3
6
1
4
5
7
2
4
5
6
8
3
5
6
4
7
8
5
7
8
col_ ptr()
0
3
7
10
14
19
22
25
28
Для предварительной инициализации формата
CCS
необходимо заранее
определить число ненулевых коэффициентов и портрет полной матрицы. При
расчете портрета полной матрицы следует учесть, что ее ненулевые коэффициен-
ты могут складываться из нескольких коэффициентов элементных матриц, и что
Модельная сетка
















