
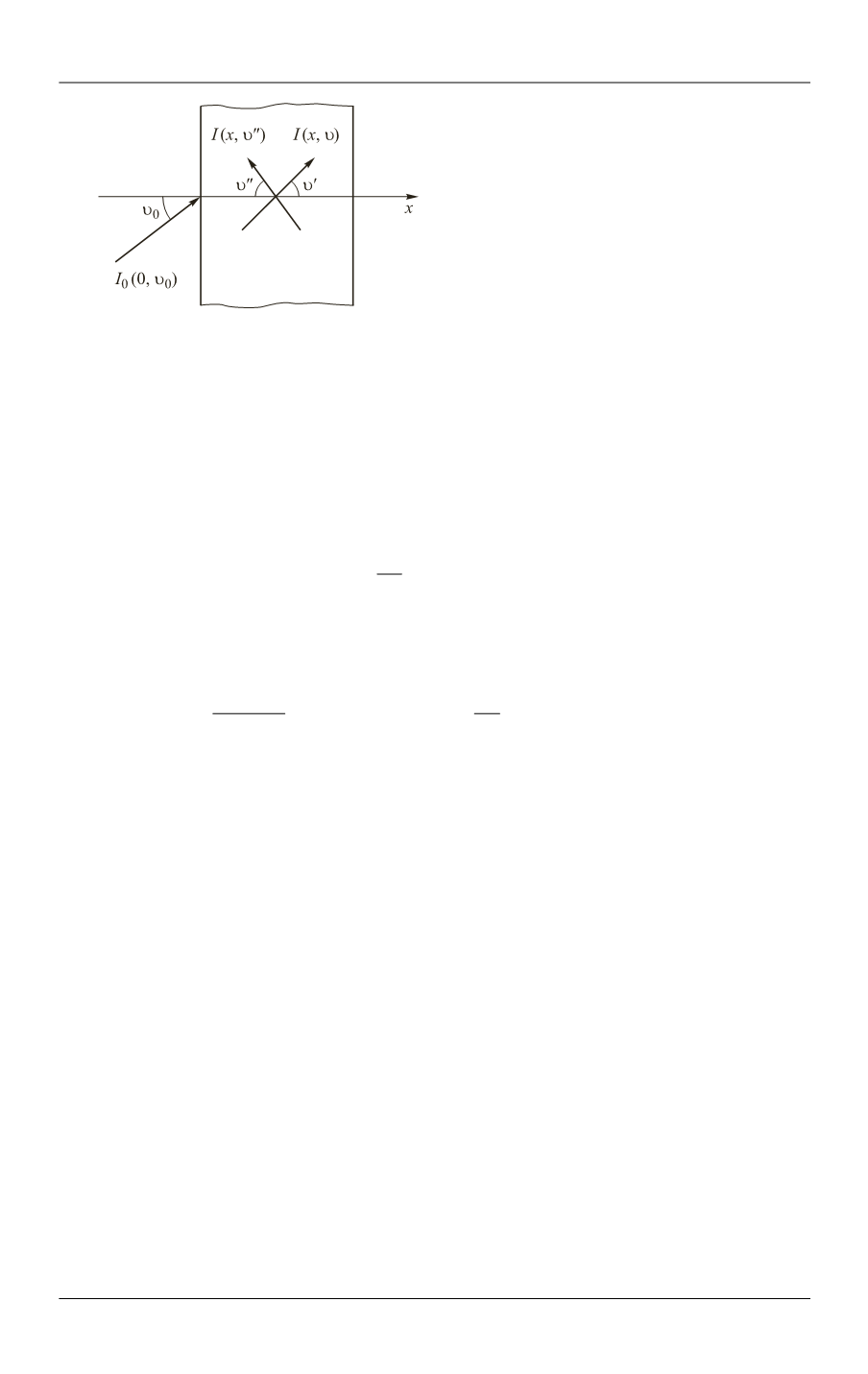
S. Persheyev, D.A. Rogatkin
84
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
Fig. 3.
Schematic ''flat'' representation
of the radiation transfer in the
multidimensional formulation
In the ''flat'' 2D representation, some radiance
I
(
x
,
) [W
sr
−1
m
−2
], where
is a
polar angle (
I
(
x
,
) also called as light intensity) propagates inside the turbid medium
at the angle
to the axis ''
X
''. For a narrow pencil of radiation, the radiance
I
(
x
,
) and
a radiant flux
F
(
x
)
are related by the equation
F
(
x
)
= I
(
x,
)cos(
) [5, 11]. However, in
the general 3D case, the flux
F
(
x
)
in a channel with a large solid angle
must be cal-
culated from the radiance
I
(
x,
) by an integration over all angles included in the
channel:
1 ( )
( , )cos
,
2
F x
I x
d
(11)
where
is the solid angle. This approach was used, for example, by D. Yudovsky and
L. Pilon [12]. Sometimes, using this approach, a ''1D'' RTE takes the form [13, 14]:
4
( , )
cos
(
) ( , )
( , ) ( ,
) .
4
s
a s
dI x
I x
p
I x d
dx
(12)
where
a
and
s
are the absorption and scattering coefficients respectively, and
( , )
p
is the scattering phase function. This approach is used since the introduction
of the Schuster and Eddington approximations [8], and is very widespread due to the
simplification of the coordinate system for RTE. However, this is not the pure 1D
formulation of the problem. It is rather some 1D projection of a multidimensional
task. It can be considered, but our objective is the pure 1D scattering problem, which
does not contain any angles and directions of a radiance propagation different from
the
X
-axis. We will consider the pure 1D turbid media, which is supposed to have
only one line for the light transport — the axis ''
X
'', and there are not various angles at
which light can travel.
Radiation penetrates the 1D turbid medium along the axis ''
X
'', and while
propagating inside the medium is absorbed by the substance of the medium and (or)
scattered by the heterogeneities of the inner structure of the medium. In the 1D
problem, light rays are characterized by only two parameters: by directions of
propagation (forward and backward), and by amplitudes, i.e. by a radiant flux with
the dimension of watt [W]. Radiant intensity [W
sr
−1
] can be used as the amplitude
characteristics of the light beam, as well, but it makes a little difference in the
reasoning and mathematical formulation of all main equations in the 1D case.
















