
A New Look at Fundamentals of the Photometric Light Transport and Scattering Theory
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
85
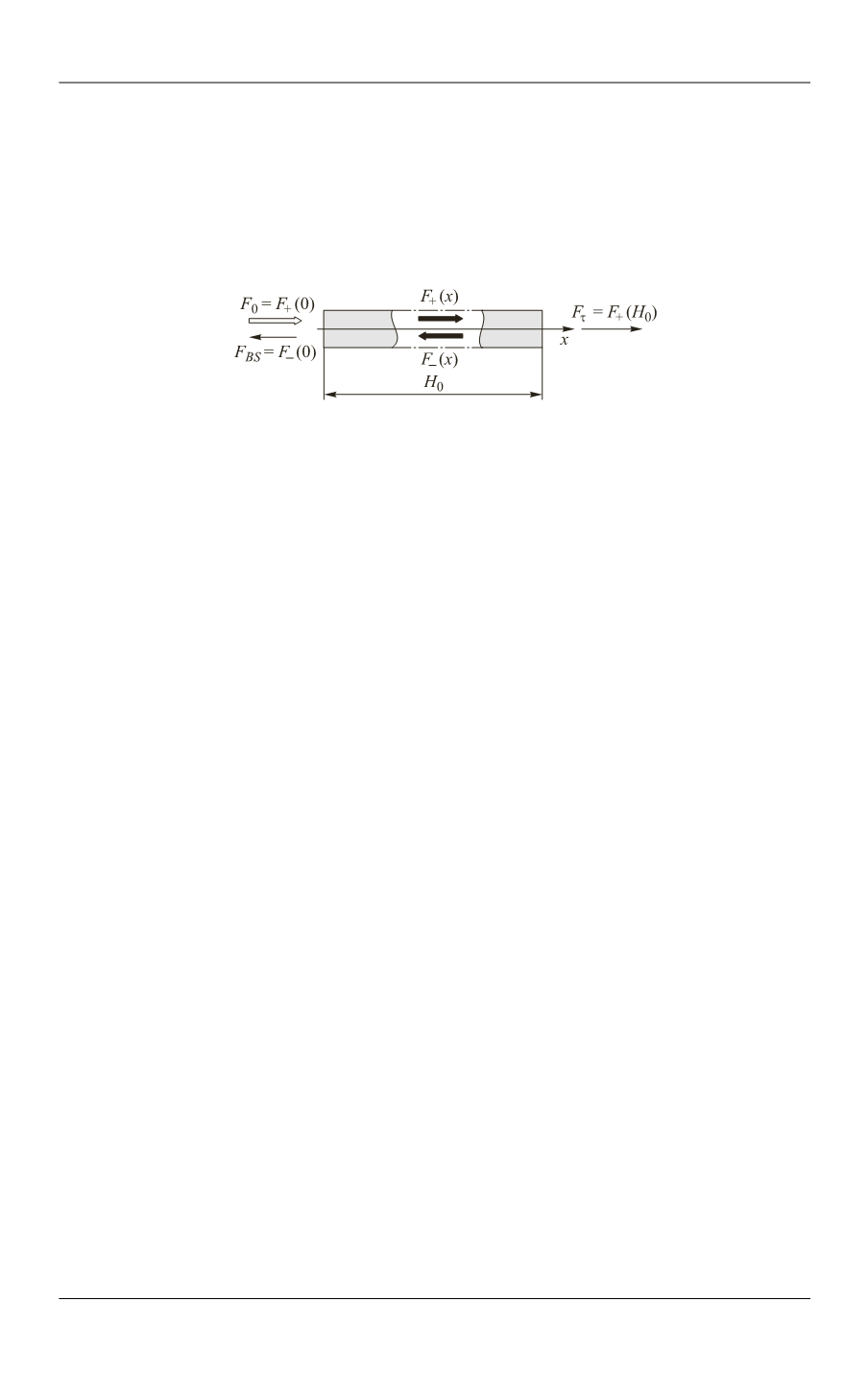
Our model of 1D turbid medium does not have a width, only a length (
H
0
).
Therefore, two fluxes only can exist inside the medium — a forward flux; we will denote
it as
F
+
(
x
), and a backward one; we will denote it as
F
−
(
x
). In Figures, it is quite difficult to
present a pure 1D scheme of light propagation, so for visibility to show propagating
fluxes and some nuances of their scattering inside the medium we will illustrate the
medium by a ''thin'' stick. An example of such a representation is shown in Fig. 4.
Fig. 4.
Schematic representation of the 1D medium and
propagating fluxes inside and outside it
The concept of diffraction of radiation in the 1D case has no any sense, because
the diffraction is fundamentally a multidimensional phenomenon. In the 1D case, the
scattering phase function is degenerated to the single opposite direction only, i.
e.
actually also does not exist (may not be taken into account). In the 1D problem, the
only process that should be under consideration as scattering is the back-reflection of
fluxes on ''dotted'' inhomogeneities along the
X
-axis. It is important to note here, that
scattering as reflections is a discrete process on discrete inhomogeneities in principle.
All it makes the problem to be effortless solved analytically in the closed form. The
common approach used to solve the problem consists in formulation of differential
equation for radiant fluxes changes at propagation inside a medium. We will use this
technique, as well.
Pure scattering.
As the first step, we will consider the case of the pure scattering.
This is the limit case of the absence of absorption inside the turbid medium. From the
electromagnetic point of view, it is the case of the perfect dielectric medium.
Imaginary part of the refractive index inside the medium
= 0. Therefore,
K
= 0, so
only scattering will take place. As we have mentioned above, we suspect there is an
inaccuracy in the definition of the scattering coefficient in LT&ST, and in
incorporation of it into RTE. Therefore, the investigation on the scattering coefficient
formation in a common phenomenological approach is more interesting for us. Pure
scattering approximation give the best opportunity for the study. Thus, our task is to
calculate a backscattered flux
)0( ,
BS
F F
as well as a transmitted flux
0
( )
F F H
as
functions of optical properties of the medium. In the case of 1D pure scattering
media, there are only a few physical properties of the media — a length
0
,
H
a
number
N
of inhomogeneities distributed along the
X
-axis inside the medium, and
the reflectivity
R
i
for each
i
-th inhomogeneity.
Assume all
R
i
= const =
R
. For a formation of the scattering coefficient item, it
does not matter. Let all
N
inhomogeneities
i
r
be uniformly or some kind randomly
distributed inside the medium. Figure 5 demonstrates the uniform distribution.
















