
О.В. Щерица, А.О. Гусев, О.С. Мажорова
120
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
менное определение положения границы раздела фаз, распределения темпера-
туры и массы в системе. Предложенный метод применяется для численного ис-
следования процессов роста и растворения соединений
1
A B C.
x x
Постановка задачи.
Рассмотрим задачу о кристаллизации тройного соедине-
ния
1
A B С.
x x
Раствор компонентов A и B в расплаве
C
приводится в контакт с
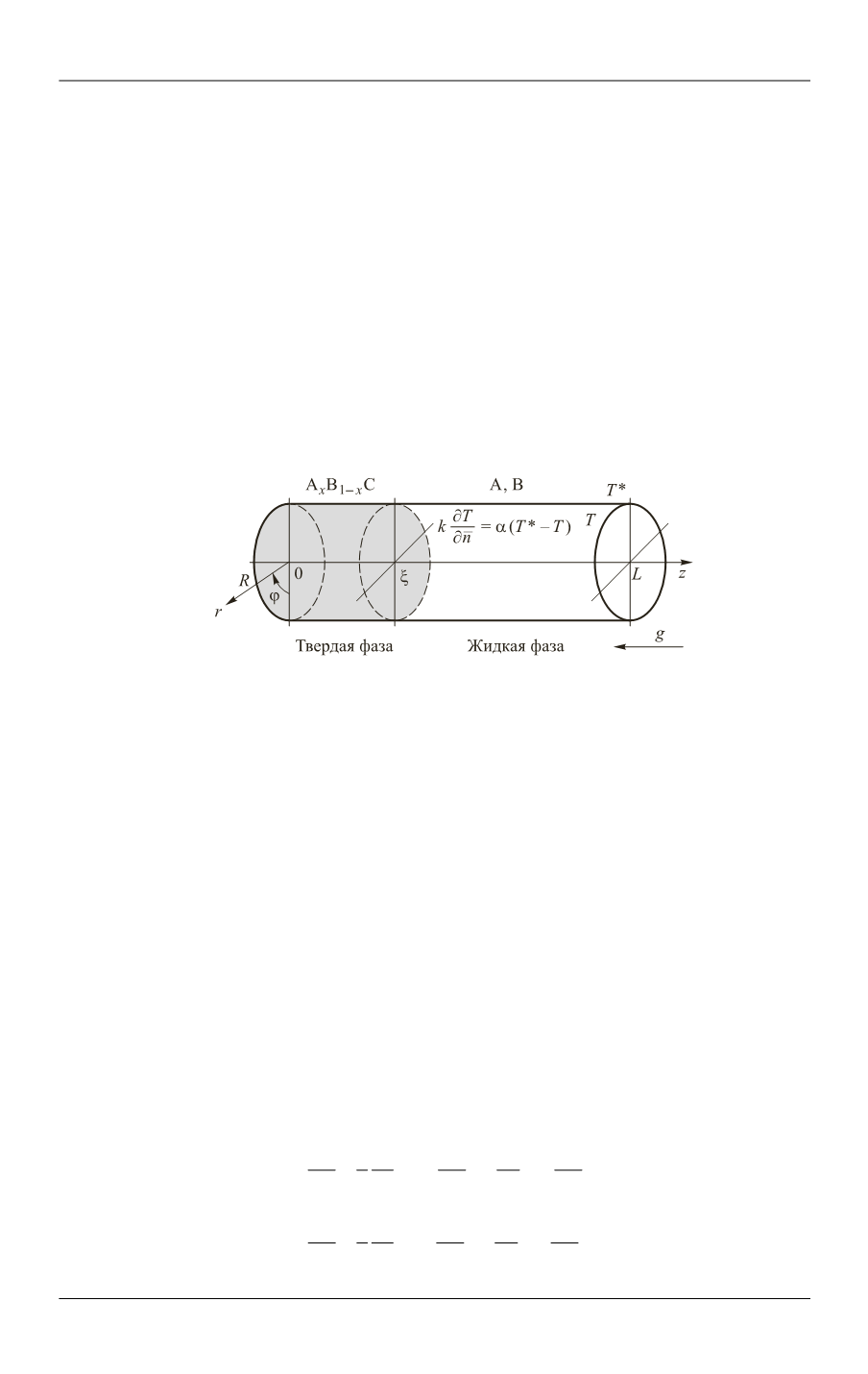
затравкой, расположенной на дне тонкой цилиндрической ампулы (рис. 1). Затем
температура системы понижается, жидкая фаза становится пересыщенной, и начи-
нается процесс кристаллизации. Математическое моделирование проводится в
рамках следующих предположений. На фронте кристаллизации состав жидкой и
твердой фазы находится в квазиравновесии. Кинетические процессы на поверхно-
сти протекают достаточно быстро и не нарушают квазиравновесия. Фронт кри-
сталлизации плоский. Конвекция в жидкой фазе незначительна, тепломассопере-
нос в системе осуществляется механизмом диффузии.
Рис. 1.
Цилиндрическая ампула
Подобласть
=( , ] (0, ],
l
L R
где
L
— длина ампулы;
= ( )
t
— положение
фронта кристаллизации;
R
— радиус ампулы (см. рис. 1), занимает жидкая фа-
за, которая представляет собой раствор компонентов A и B в расплаве
C.
Со-
став жидкой фазы определяется концентрациями компонентов A и
B,
а кон-
центрация вещества
С
вычисляется из условия
(A)
(B)
(C)
=1,
l
l
l
x x x
где
( )
,
l j
x
= A, B, C
j
— мольная доля соответствующего компонента в жидкой
фазе. Твердая фаза занимает область
=[0, ) (0, ]
s
R
и является твердым рас-
твором
1
A B С.
x x
Состав твердой фазы определяется одной переменной
,
x
при
этом мольные доли каждого ее компонента
( )
,
s j
x
= AC, BC,
j
удовлетворяют
соотношениям
(AC)
(BC)
,
1 .
s
s
x
x x
x
(1)
Распределение температуры и состава в системе описывается уравнениями
1=
, ( , )
;
t
s s
s
s
p
s
T
T
T
c
rk
k
z r
r r
r
z
z
(2)
1=
, ( , )
.
t
l
l
l
l
p
l
T
T
T
c
rk
k
z r
r r
r
z
z
(3)
















