
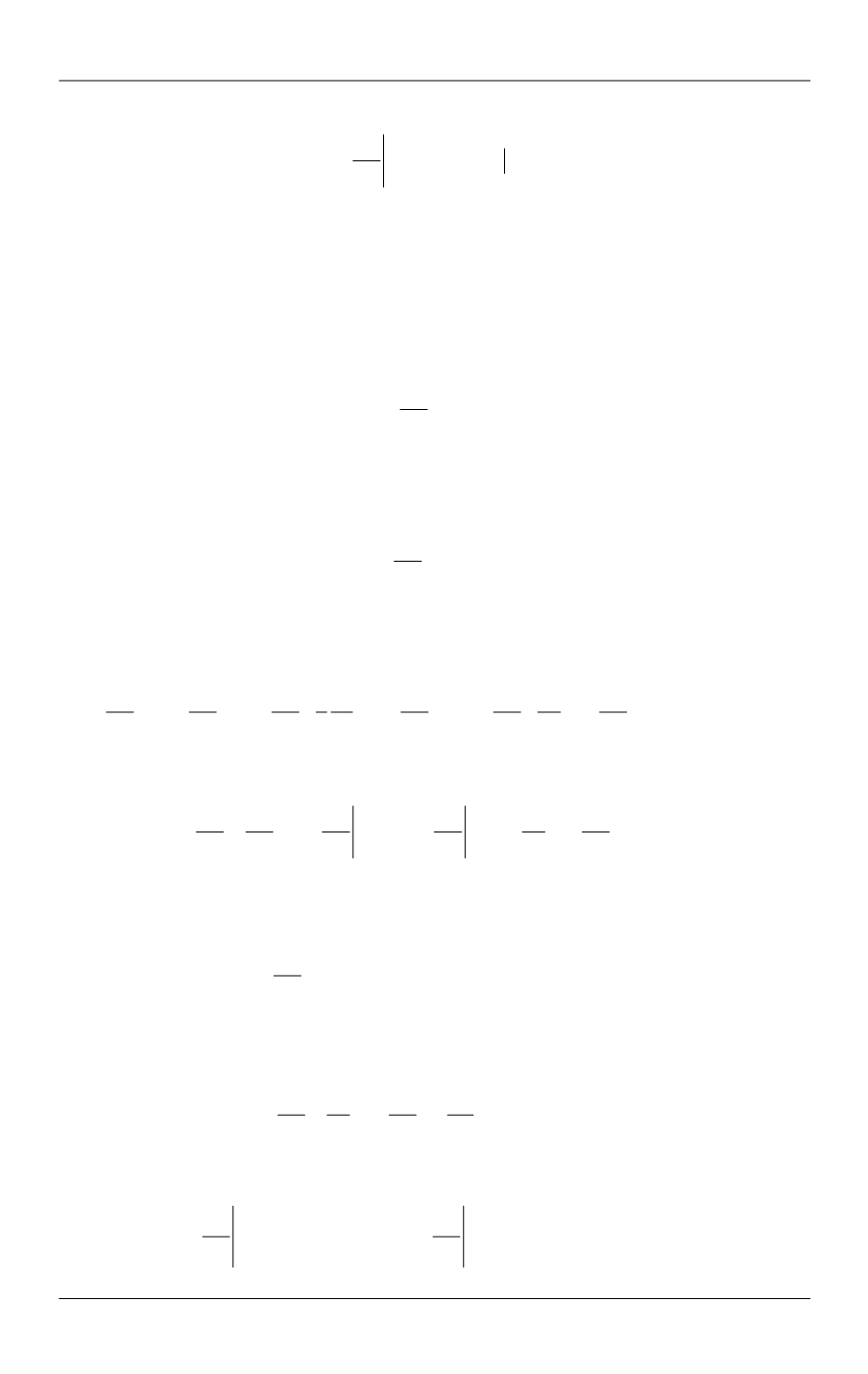
О.В. Щерица, А.О. Гусев, О.С. Мажорова
122
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
На поверхности цилиндра происходит теплообмен по закону Ньютона
*
= (
).
T k
T T
n
(11)
Здесь
— коэффициент контактного теплообмена;
*
T
— температура окру-
жающей среды.
Состояние системы можно описать функциями
( , t)
T z
и
( )
( , t),
j
C z
=A, B,
j
= , ,
s l
где
1)
( , t)
T z
— средняя температура в сечении
z
в момент времени
t :
2
0
2
( , t)
( , , t) ;
R
T z
T r z rdr
R
(12)
2)
( )
( , t)
j
C z
— средняя концентрация компонента
j
( = A, B, = , )
j
s l
в се-
чении
z
в момент времени t:
( )
( )
2
0
2
( , t)
( , , t) .
R
j
j
C z
C r z rdr
R
Для того чтобы получить уравнение для температуры
( , ),
T z t
проинтегри-
руем (2), (3) по радиусу
:
r
2
2
2
0
0
0
2
2 1
2
=
,
= , ,
t
R
R
R
p
T
T
T
c
rdr
k r
rdr
k
rdr
s l
r r
r
z
z
R
R
R
с учетом (12) получим
2
=
=0
2=
,
= , .
t
p
r R
r
T
T
T
T
c
k r
k r
k
s l
r
r
z
z
R
(13)
Поскольку значение температуры на боковой поверхности цилиндра не за-
висит от его радиуса, верно соотношение
2
0
2 ( , , t)
( , , t) ( , t),
R
T R z rdr T R z T z
R
что позволяет переписать (13) с учетом граничных условий на боковой поверх-
ности (11) в виде
*
2
=
(
),
= , .
t
p
T
T
c
k
T T
s l
z
z R
(14)
Граничные условия на торцах ампулы
*
*
=0
=
= (
),
= (
),
= , .
z
z L
T
T
k
T T k
T T
s l
z
z
(15)
















