где
a
k
(
z
i
)
π
=
a
ik
π
=
a
ik
0
,
¯
p
k
=
2
p
k
G
a
u
a
0
.
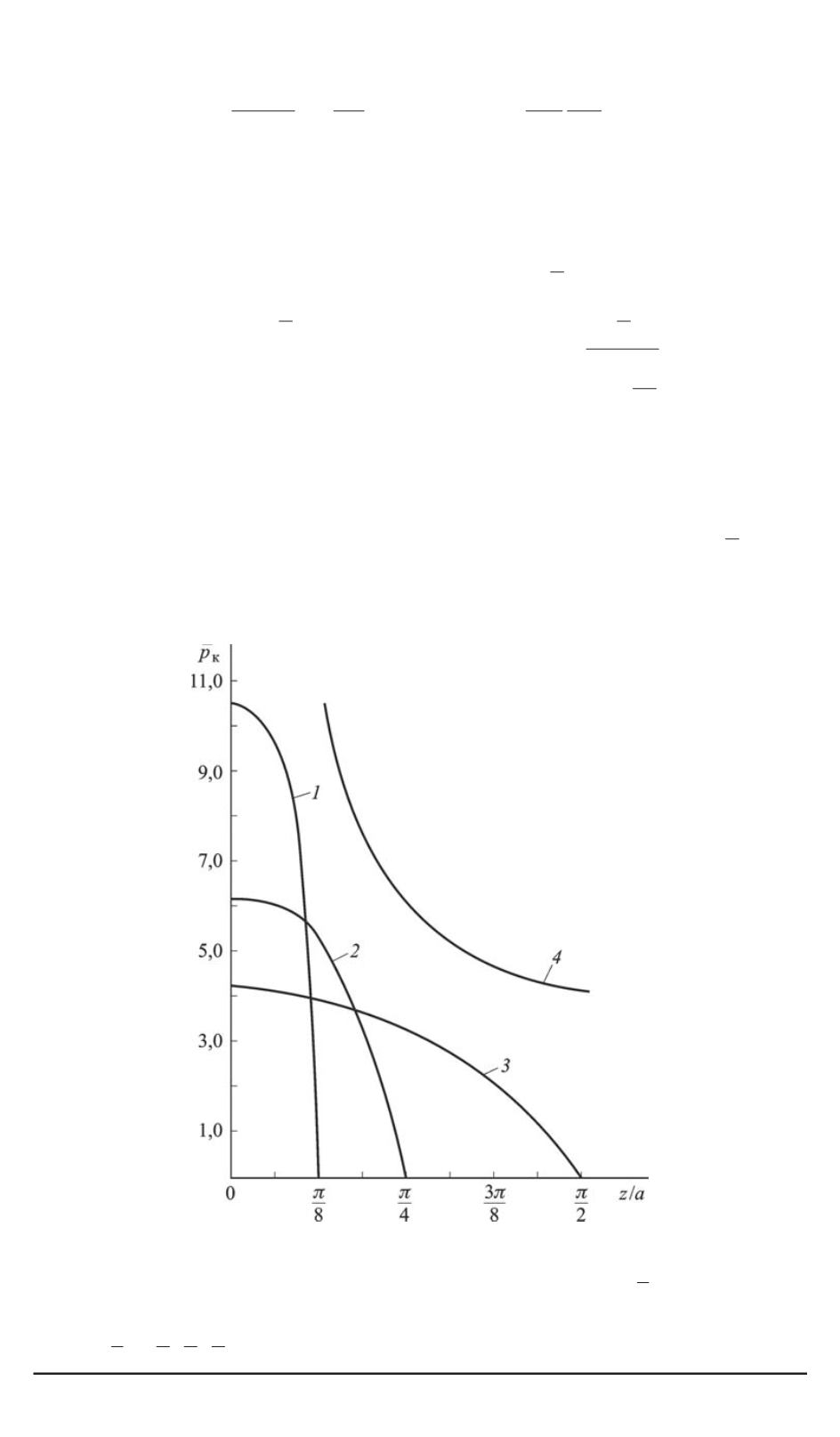
Проведенные расчеты определения давления в зоне контакта дви-
жущегося твердого тела с внутренней поверхностью цилиндра при
параболическом профиле тела позволили получить зависимость вели-
чины давления от ширины области контакта
2
с
a
. На рис. 1 приведены
зависимости
¯
p
k
=
f
z
a
при различных значениях
c
a
и значении па-
раметра скорости движущейся нагрузки
γ
= 1
−
v
2
c
2
2
= 0
,
8
(
c
2
—
скорость волны сдвига). Ввиду симметрии задачи на рис. 1 показана
только правая половина зависимостей. Кривые строились при фикси-
рованных значениях толщин полого цилиндра
(
b/a
)
и скорости дви-
жения твердого тела (параметр
γ
)
. При сокращении ширины
c
a
в два
раза максимальное давление
¯
p
ko
= ¯
p
k
=0
увеличивается в 1,5 и более
раз.
Рис. 1. Графики распределения контактного давления
¯
p
k
(кривые
1, 2, 3
) и мак-
симального давления
¯
p
k
0
(
4
) по осевой координате цилиндра
z
a
при различных
значениях полуширины зоны контакта
c/a
(
b/a
= 3;
γ
= 0
,
8
):
1, 2, 3
-
c
a
=
π
8
,
π
4
,
π
2
соответственно
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 1
59


