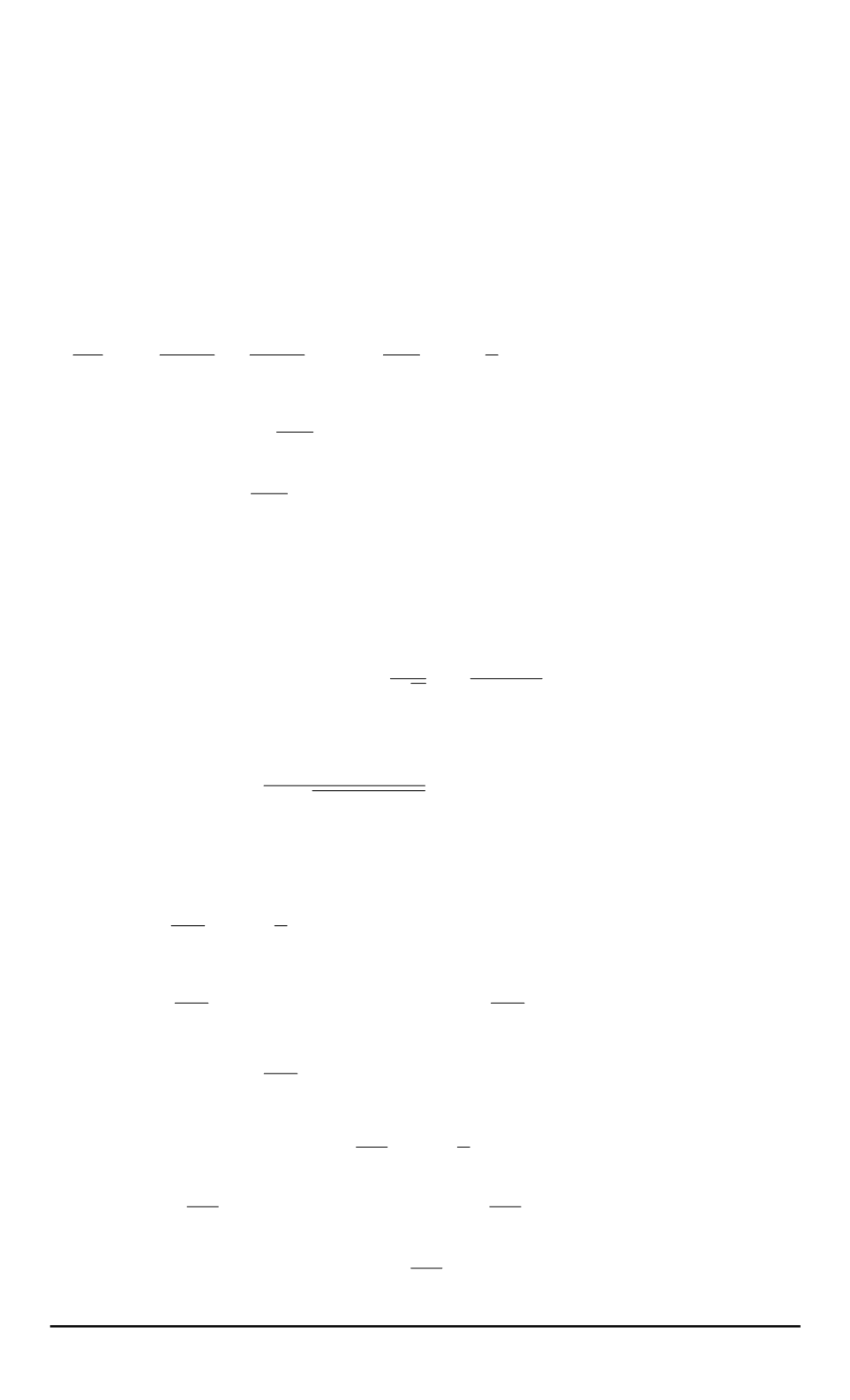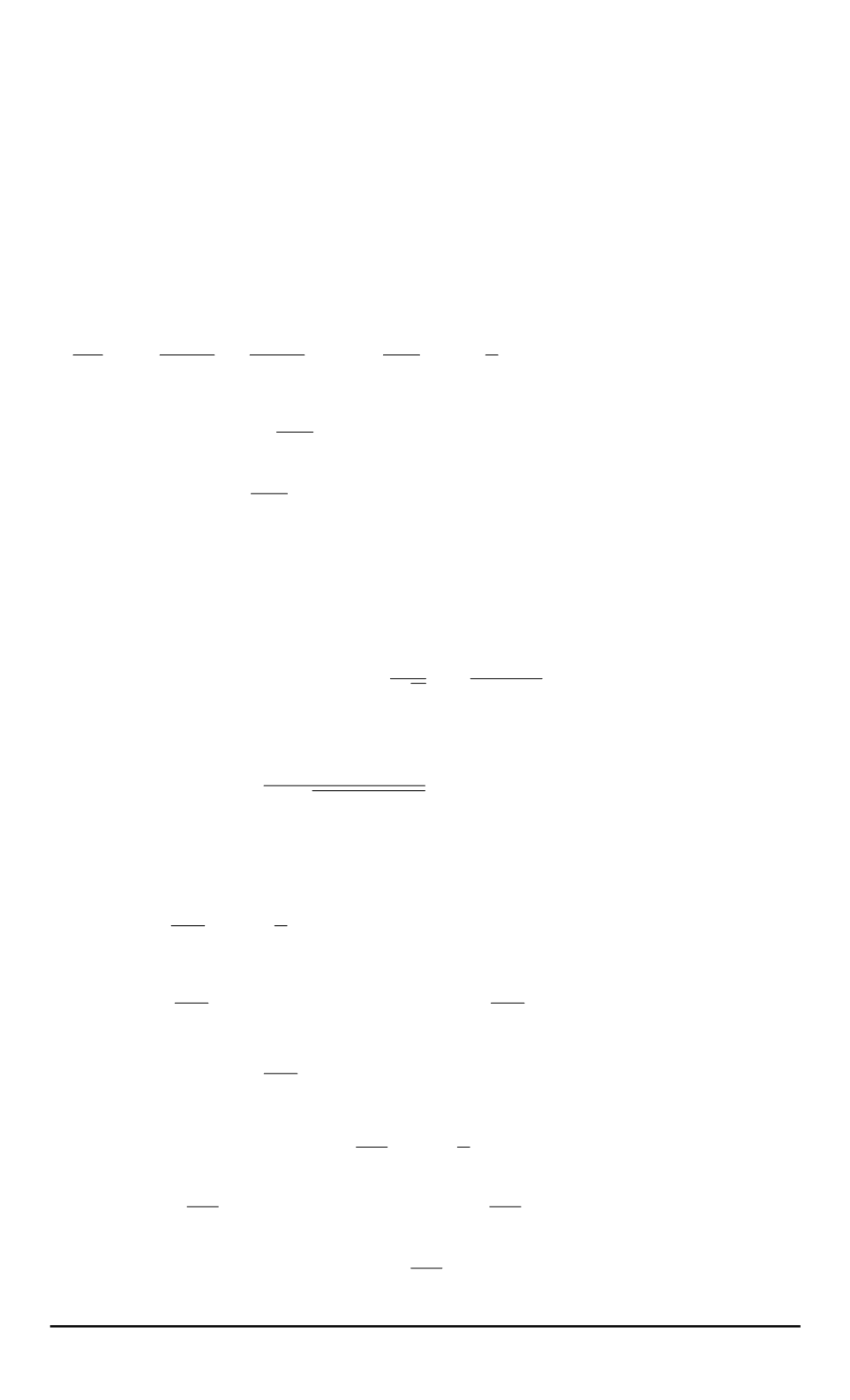
Так как для рассматриваемых дрейфовых волн
kr
D
1
(
r
D
— деба-
евский радиус), то вместо уравнения Пуассона используется условие
квазинейтральности
X
α
=
i,e
q
α
Z
f
1
α
d
3
v
= 0
.
(3)
Интегрируя соотношение (2) по скоростям, находим отношение
возмущения концентрации частиц сорта
α
к невозмущенному значе-
нию
n
α
n
α
=
−
q
α
ϕ
k
B
T
α
−
q
α
ϕ
k
B
T
α
1 +
ω
α
ω
1
−
3
2
η
α
Γ
0
(
b
α
)
ξ
α
Z
(
ξ
α
)+
+
ω
α
ω
η
α
Γ
0
(
b
α
)
ξ
α
ξ
α
+
ξ
2
α
Z
(
ξ
α
) +
+
ω
α
˜
ω
η
α
Γ
0
(
b
α
) +
b
α
Γ
1
(
b
α
)
−
b
α
Γ
0
(
b
α
)
ξ
α
Z
(
ξ
α
)
.
(4)
Здесь
Γ
n
(
b
) =
I
n
(
b
) exp(
−
b
)
;
I
n
(
b
)
— модифицированные функции Бес-
селя;
b
α
=
k
2
?
ρ
2
Tα
;
ρ
Tα
=
m
α
v
Tα
/
(
|
q
α
|
B
)
— ларморовский радиус, вы-
числяемый по тепловой скорости частиц данного сорта;
Z
(
ξ
) =
1
√
π
∞
Z
−∞
e
−
u
2
du
u
−
ξ
(5)
— плазменная дисперсионная функция, аргумент которой для частиц
сорта
α
равен
ξ
α
=
ω
k
||
p
2
k
B
T
α
/m
α
.
Используя условие квазинейтральности (3), получаем дисперсион-
ное уравнение для дрейфовых волн в виде
1 + 1
−
ω
e
ω
1
−
3
2
η
e
ξ
e
Z
(
ξ
e
)Γ
0
(
b
e
)
−
−
ω
e
ω
η
e
ξ
e
[
ξ
e
+
ξ
2
e
Z
(
ξ
e
)]Γ
0
(
b
e
)
−
ω
e
ω
η
e
ξ
e
Z
(
ξ
e
)Γ
0
(
b
e
)
−
−
ω
e
ω
η
e
ξ
e
Z
(
ξ
e
)
b
e
[Γ
1
(
b
e
)
−
Γ
0
(
b
e
)] =
=
−
τ
1 + 1 +
ω
i
ω
1
−
3
2
η
i
ξ
i
Z
(
ξ
i
)Γ
0
(
b
i
)+
+
ω
i
ω
η
i
ξ
i
[
ξ
i
+
ξ
2
i
Z
(
ξ
i
)]Γ
0
(
b
i
) +
ω
i
ω
η
i
ξ
i
Z
(
ξ
i
)Γ
0
(
b
i
)+
ω
i
ω
η
i
ξ
i
Z
(
ξ
i
)
b
i
[Γ
1
(
b
i
)
−
Γ
0
(
b
i
)]
,
(6)
24
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 1