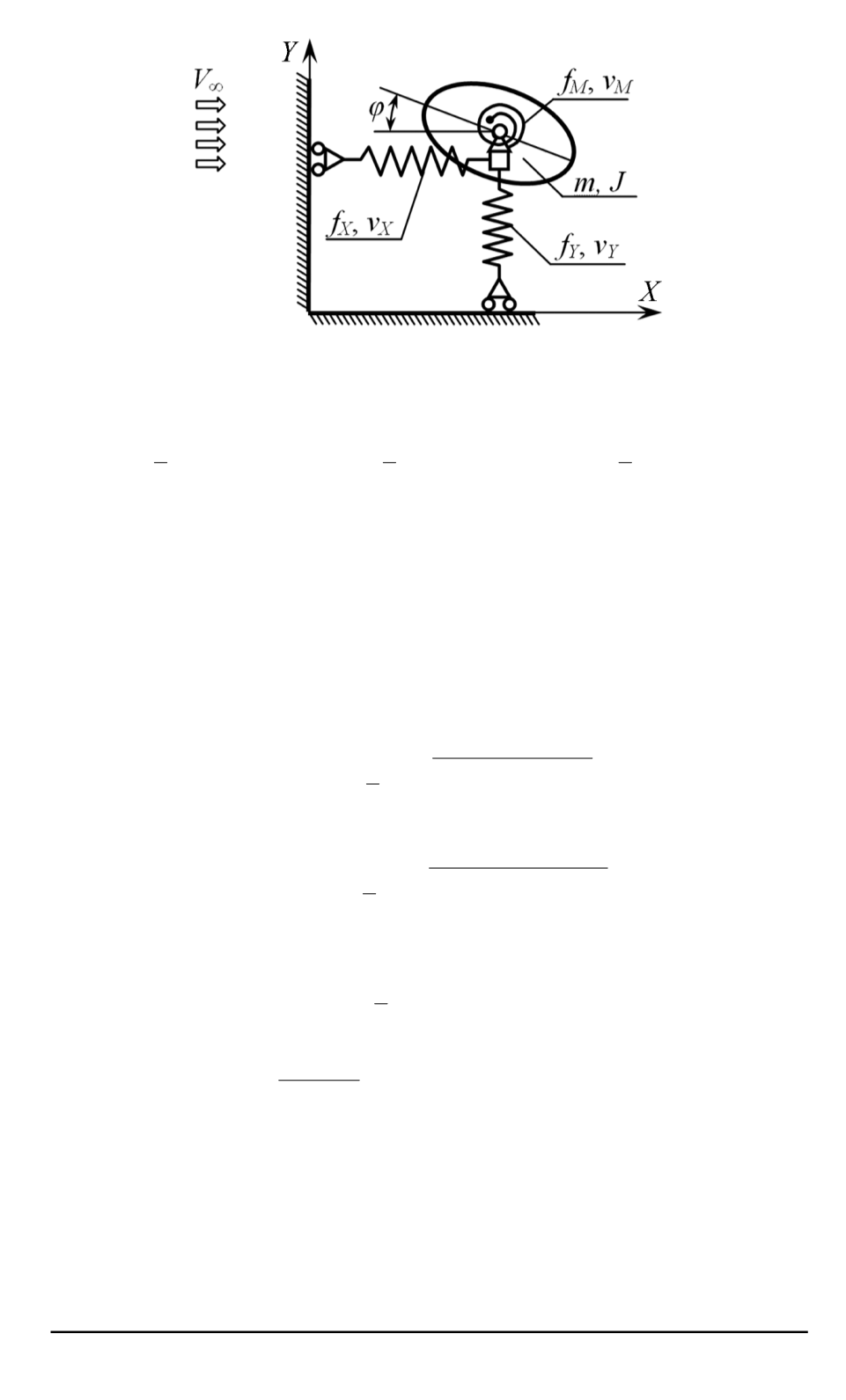
Рис. 2. Расчетная схема эксперимента
кого момента, которые вычисляются по формулам
X
a
=
1
2
C
Xa
ρ
V
2
rel
S
;
Y
a
=
1
2
C
Y a
ρ
V
2
rel
S
;
M
a
=
1
2
C
Ma
ρ
V
2
rel
S
2
,
где
ρ
— плотность воздуха,
V
rel
— относительная скорость набегаю-
щего потока,
S
— характерный линейный размер (хорда) профиля.
Принято допущение, что безразмерные аэродинамические коэф-
фициенты
C
Xa
,
C
Y a
и
C
Ma
для данного профиля стационарные, т.е.
зависят явно только от угла атаки профиля
ϕ
, и эти зависимости непре-
рывно дифференцируемы. В этом случае система дифференциальных
уравнений, описывающих движение профиля в потоке, имеет вид
m
¨
x
+
ν
X
˙
x
+
f
X
x
=
1
2
ρ
S
q
(
V
∞
− ˙
x
)
2
+
˙
y
2
×
×
[
C
Y a
(α)
∙ ˙
y
+
C
Xa
(α)
∙
(
V
∞
− ˙
x
)
]
,
m
¨
y
+
ν
Y
˙
y
+
f
Y
y
=
1
2
ρ
S
q
(
V
∞
− ˙
x
)
2
+
(
˙
y
)
2
×
×
[
C
Y a
(α)
∙
(
V
∞
− ˙
x
)
−
C
Xa
(α)
∙ ˙
y
]
,
J
¨
ϕ
+
ν
M
˙
ϕ
+
f
M
ϕ
=
1
2
ρ
S
2
(
V
∞
− ˙
x
)
2
+
˙
y
2
C
Ma
(α) .
(3)
Здесь
α
=
ϕ
−
arctg
˙
y
V
∞
− ˙
x
, точкой обозначена производная по вре-
мени.
При любой скорости набегающего потока
V
∞
существует хотя бы
одно положение равновесия профиля
x
=
x
0
,
y
=
y
0
,
ϕ
=
ϕ
0
, и
основная цель настоящей работы — исследование устойчивости по
Ляпунову такого положения равновесия. Для этого запишем систему
уравнений первого приближения. Считая координаты и скорости про-
филя малыми, можно линеаризовать исходную нелинейную систему
32
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4


