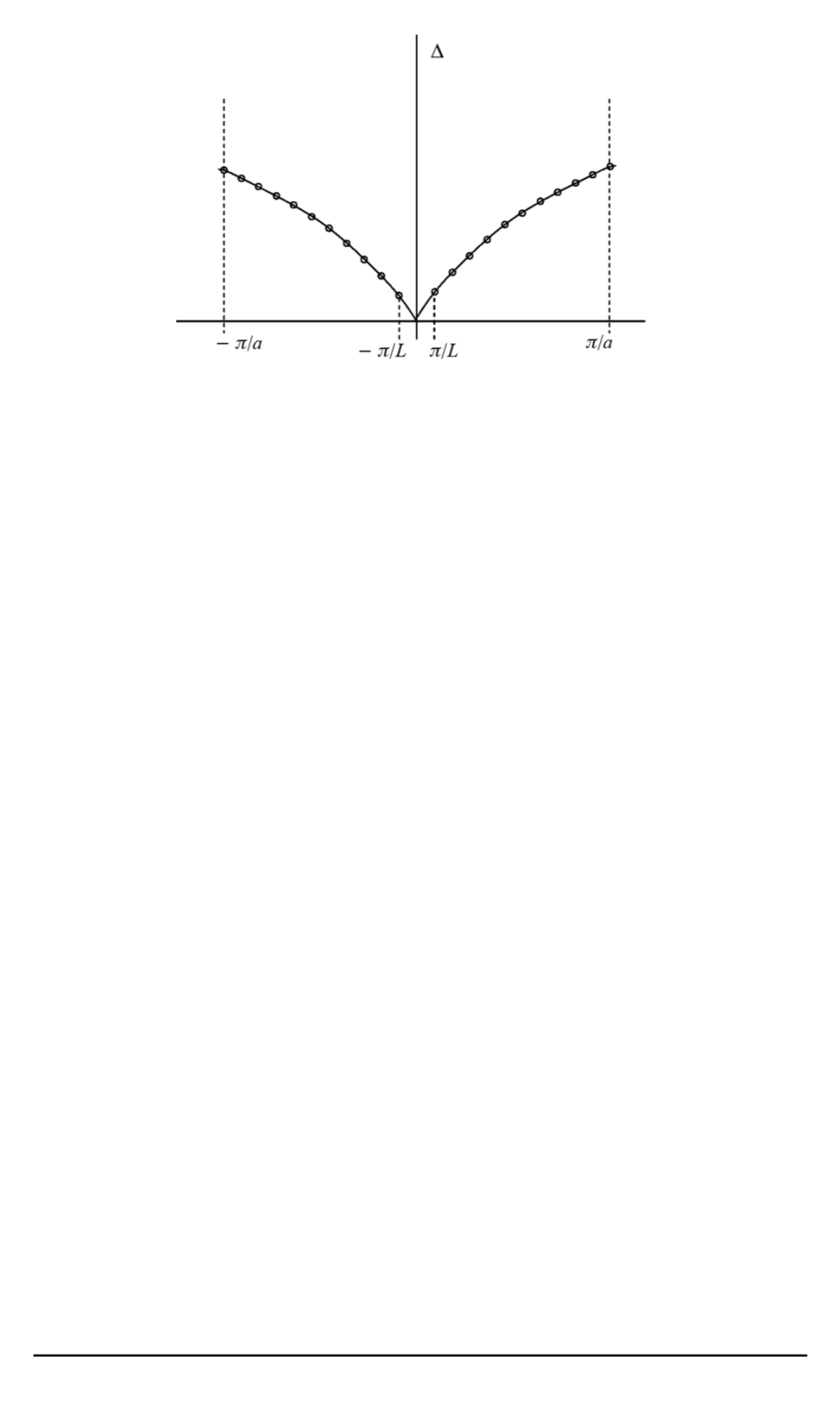
Рис. 8. Дисперсионная кривая микрорезонатора в фотонном кристалле, содер-
жащем плоские дефекты
Введение
n
eff
соответствует модели оптического резонатора с плоски-
ми зеркалами, заполненного средой с эффективным показателем пре-
ломления, который рассчитывался по формуле
n
2
eff
= (1
−
η
)
n
2
1
+
η n
2
2
,
(9)
где
n
1
и
n
2
— показатели преломления сфер из SiO
2
и полостей
между ними,
η
— относительный объем полостей (для идеальной
ГЦК-решетки
η
= 0
,
25)
.
Числовая оценка величины
Δ
E
при
N
= 1
, n
eff
= 1
,
26
и
L
= 50
мкм
дает
Δ
E
= 0
,
0156
эВ.
В случае учета упорядоченной структуры глобулярных кластеров
внутри кристаллита необходимо учесть условие
L
=
N
1
a,
(10)
приводящее к следующему виду формулы (8):
Δ
E
= ((
chn
eff
cos
α
)
/
2
N
1
a
)
N.
(11)
Рассмотрим предельный случай
cos
α
= 1
для формулы (11), когда
N
=
N
1
, т.е. ширина кристаллита равна постоянной решетки. Тогда
имеем
Δ
E
=
hcn
eff
/
2
a.
(12)
Эта формула определяет максимальную энергию кванта возбуждения.
Если постоянная решетки
a
= 0
,
2
. . .
0
,
6
мкм, то
Δ
E
max
= 1
,
3
. . .
3
,
9
эВ.
Используя условие
N
= 1
при выполнении равенства
a
= 0
,
2
мкм и
применяя формулу (8) к обработке приведенных экспериментальных
данных, получаем следующие оценки:
L
= 5
,
8
; 6,5; 7,4; 8,6 мкм в
случае скользящего падения луча и
L
= 4
,
2
;
5
,
4
;
6
,
6
;
10
,
9
;
33
,
6
мкм
для проходящего излучения и наклоне образца на угол
15
◦
от напра-
вления нормального падения. Расстояния между плоскими дефектами
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 3
91


