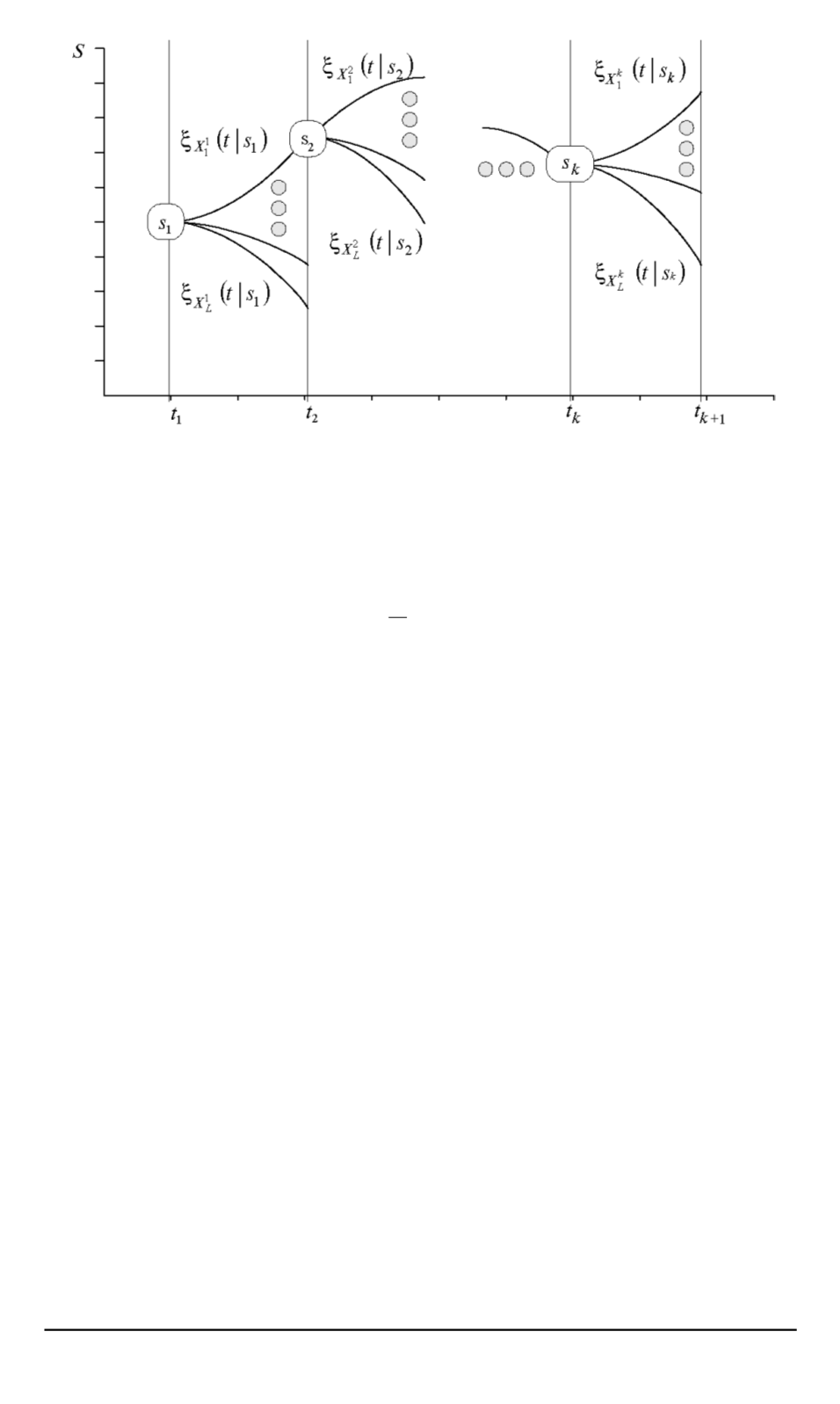
Схема выбора режимов управления
3. Вычисляются среднеинтегральные оценки характеристик для
всех
l
= 1
, . . . , L
при общем начальном состоянии
s
k
:
ˆ
Y
X
k
l
(
T
) =
1
T
T
Z
0
ξ
X
k
l
(
t
|
s
k
)
dt.
(5)
4. Вычисляются оценки координат вектора
ˆ
β
k
— градиента функции
характеристик
Y
(
X
k
)
.
5. Выбирается очередное значение режима управления
X
k
+1
=
X
k
+
a
k
ˆ
β
k
,
(6)
где
a
k
— расходящийся ряд (обычно гармонический).
6. Задается начальное состояние
s
k
+1
следующего интервала упра-
вления, равное конечному состоянию одного из процессов предыду-
щего шага.
7. В соответствии с выбранным критерием останова выполняется
переход к п. 2, либо к окончанию моделирования.
Таким образом, для решения поставленной задачи оптимизации
режимов управления транспортной или технологической машиной не-
обходимо знать поведение:
— основного параметризуемого процесса
ξ
X
(
t
|
s
)
, или процесса ха-
рактеристик передвижения машины;
— процесса среднеинтегральных оценок характеристик
ˆ
Y
(
T
|
s
)
;
— случайного процесса управления
η
(
t
)
— режима передвижения
транспортной либо технологической машины.
Рисунок иллюстрирует описанный выше алгоритм.
122
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 1


