Введение.
В современных разгонных блоках обеспечение сплош-
ности компонентов топлива обеспечивается за счет фазоразделяющих
экранов [1]. В связи с этим определенный интерес представляет ис-
следование малых движений жидкости, заполняющей цилиндриче-
ский сосуд, сквозь фазоразделяющие перегородки. В настоящей рабо-
те будем моделировать течение жидкости с линейным сопротивлением
сквозь такой экран и обобщим результаты [2, 3] для случая движения
двухслойной жидкости сквозь сопротивление. В работе [4] исследова-
но движение идеальной, несжимаемой и нестратифицированной жид-
кости совместно с упругим днищем, в статье [5] — вопросы устойчи-
вости свободной поверхности жидкости в условиях малой гравитации.
Свободные осесимметричные колебания двухслойной жидкости с не-
проницаемым разделителем исследованы в работе [6]. Схожая с поста-
новкой задачи, приведенной в работе [4], постановка задачи с иным
подходом к решению дифференциального уравнения движения пла-
стины реализована в работе [7]. Работа [8] посвящена исследованию
движений стратифицированной жидкости совместно с упругим дни-
щем, рассматриваемым в виде пластины, работы [9, 10] — исследова-
нию колебаний многослойных жидкостей и разделяющих мембран. В
работе [11] задача о движении стратифицированной жидкости, разде-
ленной мембраной, рассмотрена с применением операторных методов
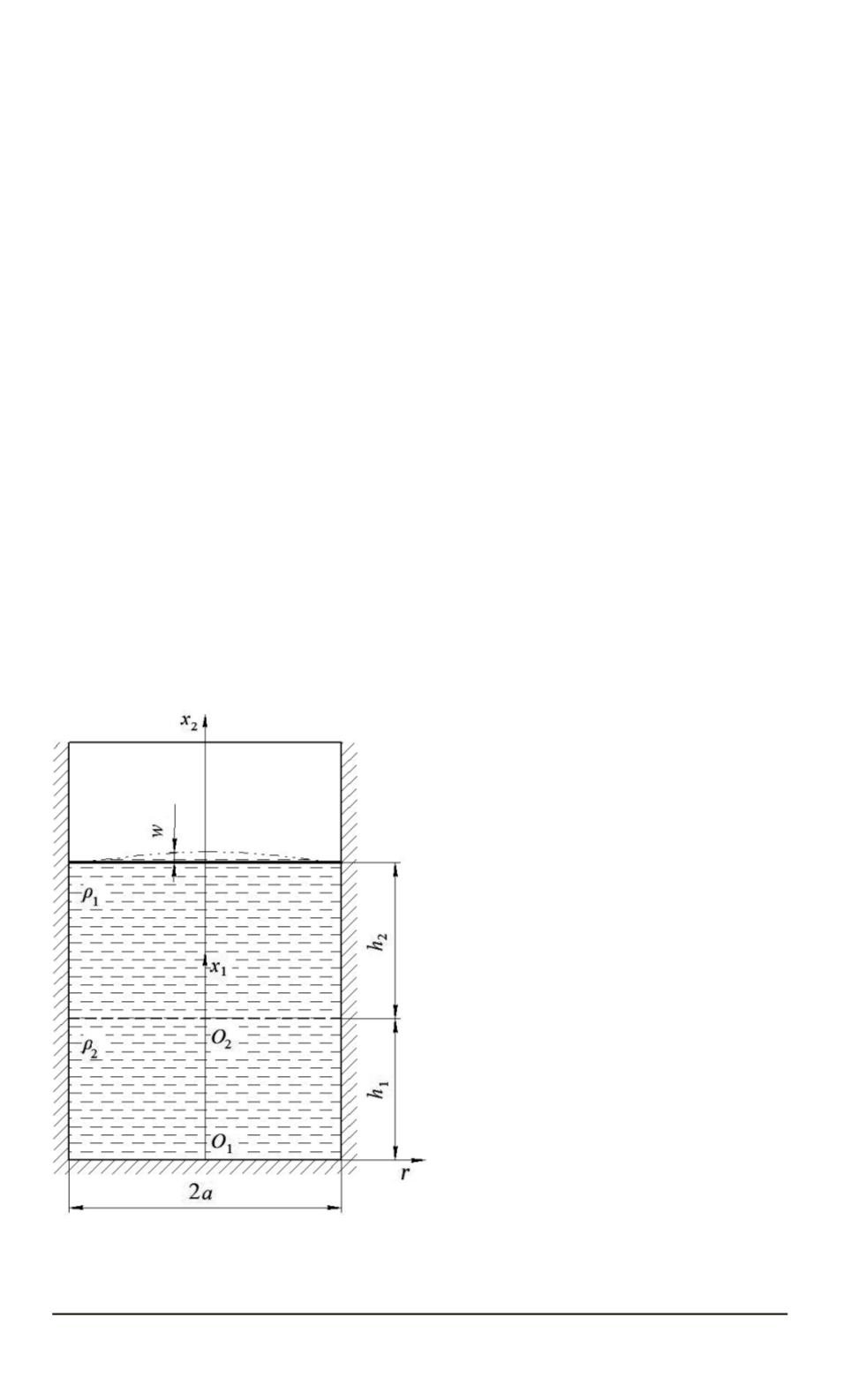
Рис. 1. Двухслойная жидкость, разделен-
ная диафрагмой
и исследованием свойств спек-
тра. В работе [12] были ис-
следованы колебания оболоч-
ки при протекании жидкости
сквозь проницаемую перегород-
ку, в работе [13] — колеба-
ния упругой проницаемой пере-
городки, взаимодействующей с
жидкостью. В работах [14–16]
изложены аспекты эксперимен-
тальных исследований разделя-
ющих экранов.
Постановка задачи.
Рассмо-
трим малые движения идеаль-
ной несжимаемой двухслойной
жидкости с плотностями
ρ
1
и
ρ
2
,
разделенной проницаемой плос-
кой диафрагмой. Введем цилин-
дрические системы координат с
началами
O
1
и
O
2
соответствен-
но (рис. 1). Движение жидкости
110
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 5


