
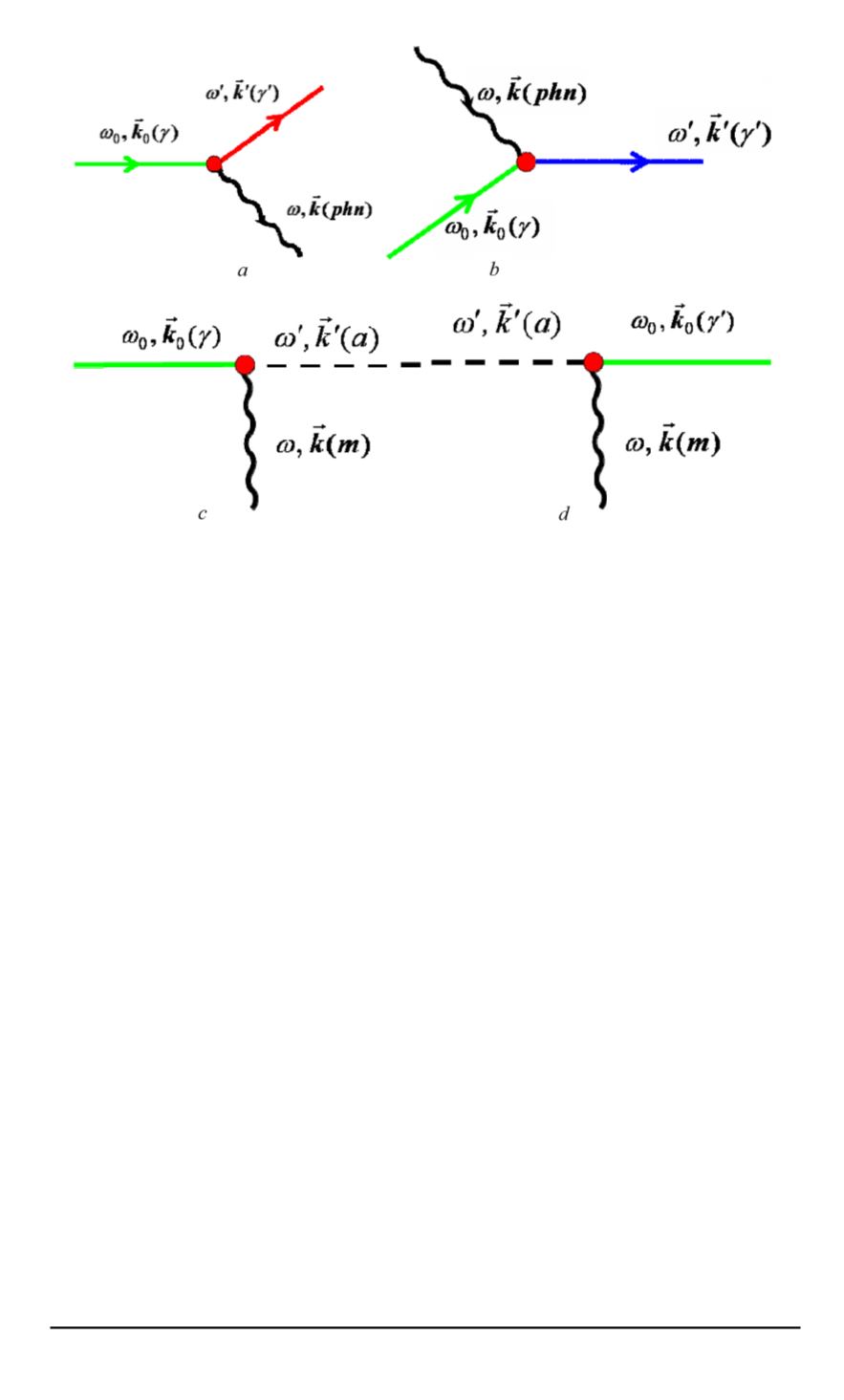
Fig. 2. Diagrams of elementary processes of Stokes CS (
a
) and anti-Stokes CS (
b
);
diagrams of photon-axion conversion processes (
c
) and axion-photon reconversion
processes (
d
)
detectors. The probability of the conversion-reconversion processes is
stipulated by the interaction constant
g
of the axional and electromagnetic
fields in vacuum, the value of
g
according to the recent estimation being
g
≈
10
−
10
GeV
−
1
.
Let us consider the processes of light combinational scattering (CS) in
crystals [10–12, 15, 21–23] as the analogue of photon-axion conversion
processes. The diagrams of elementary processes of Stokes CS and anti-
Stokes CS are shown in Fig. 2,
a, b.
In the first case A light quantum (photon) disintegrates into another
photon and a crystal quasiparticle (an optical phonon) during each CS
elementary process. The energy of the photon resulting from the inelastic
scattering action decreases. In the second case an inelastic “collision” of
the photon with the phonon occurs, which results in a photon with higher
energy. In elementary processes of Stokes SC and anti-Stokes CS, the laws
of conservation of energy and momentum (quasi-momentum) are fulfilled.
In particular, for Stokes CS (Fig. 2,
a
) the following equations are used:
~
ω
0
=
~
ω
0
+
~
ω
;
~
~k
0
=
~
~k
0
+
~
~k.
(1)
Here
~
ω
0
,
~
ω
0
,
~
ω
are the energies of exciting radiation photons, scattered
radiation and an optical phonon of the crystal;
~
~k
0
,
~
~k
0
,
~
~k
are the
corresponding momentums (quasimomentums). In the case of anti-Stokes
6
ISSN 1812-3368. Herald of the BMSTU. Series “Natural Sciences”. 2014. No. 6

















