
For solutions to equations (5) in the form of monochromatic waves
u
t
(
p
) =
u
t
(
p
)
0
exp(
ikpa
0
−
ωt
);
u
l
(
p
) =
u
l
(
p
)
0
exp(
ikpa
0
−
ωt
)
, p
= 0
,
1
,
2
, . . . ,
the following dispersion laws of the respective waves can be derived:
ω
2
t
= 4
γ
t
m
sin
2
ka
0
2
= 4
c
2
0
a
2
0
sin
2
ka
0
2
;
c
2
0
=
γ
t
m
a
2
0
;
ω
l
= 0; (
γ
l
= 0)
.
For small wave vectors
k
for transverse acoustic waves of the physical
vacuum the dispersion law can be approximated by the dispersion
relationship known in the theory of relativity for transverse electromagnetic
waves in vacuum:
ω
t
=
с
0
k
, where
с
0
=
с
t
is a velocity of transverse
electromagnetic waves (velocity of light) in vacuum. With respect to the
longitudinal acoustic waves, the initial phase of the physical vacuum
(praphase) turned out to be non-stable (
ω
l
= 0
). Cooling of the Universe
resulted in structural phase transformation and formation of superstructure
with period
a a
0
(
а
≈
10
−
15
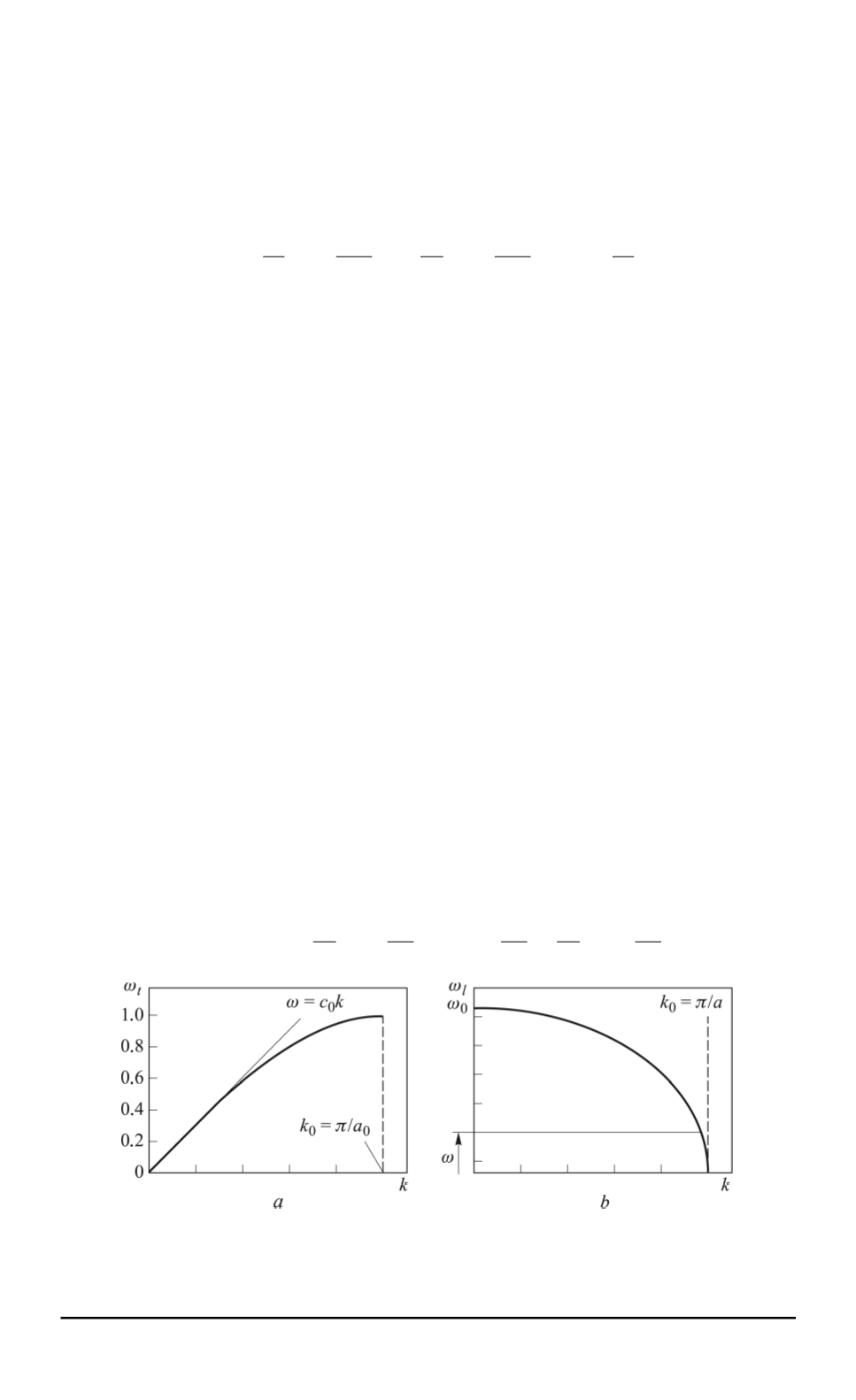
cm, Fig. 5,
b
). The dispersion law for
transverse acoustic waves in the initial (high-temperature) phase of physical
vacuum (praphase) is presented in Fig. 6,
a
.
Motion equations for translational longitudinal oscillations of the
clusters in a new (low-temperature) phase take the following form:
M
¨
u
l
(
p
) =
−
γ
0
u
l
(
p
)
−
γ
l
[2
u
l
(
p
)
−
u
l
(
p
−
1)
−
u
l
(
p
+ 1)] ;
p
= 0
,
1
,
2
, . . .
;
γ
l
<
0
, γ
0
>
0
.
A solution to equations (6) in the form of planar monochromatic waves
results in the dispersion law for longitudinal optical electromagnetic waves
(Fig. 6,
b
).
ω
2
l
=
ω
2
0
−
4
c
2
a
2
sin
2
ka
2
;
ω
2
0
=
γ
0
M
;
c
2
a
2
=
−
γ
l
M
.
(5)
Fig. 6. Dispersion laws for transverse acoustic waves in the initial phase of physical
vacuum (praphase) (
a
) and longitudinal acoustic and optical waves in vacuum after
superstructural phase transformation (
b
)
42
ISSN 1812-3368. Herald of the BMSTU. Series “Natural Sciences”. 2015. No. 1

















