
волны, за счет понижения симметрии рассматриваемой среды ока-
зываются разрешенными процессы фотон-аксионной конверсии. Та-
ким образом, при включении внешнего магнитного поля внутри по-
лярной среды возникает резонанс, задающий дополнительный полюс
ω
0
a
= 2
πc
0
ν
0
a
и дополнительный нуль
ω
1
a
= 2
πc
0
ν
1
a
диэлектриче-
ской проницаемости. Значение
ω
1
a
зависит от приложенного внешнего
магнитного поля. В связи с необходимостью учета в этом случае про-
странственной дисперсии, выражение для дисперсии диэлектрической
проницаемости метаматериала приобретает вид
ε
(
ω
) =
−
(
ω
2
l
−
ω
2
) (
ω
2
la
+
c
2
0
k
2
−
ω
2
)
ω
2
(
ω
2
0
a
+
c
2
0
k
2
−
ω
2
)
.
(6)
Подставляя (6) в (3), получаем биквадратное уравнение для закона
дисперсии
ω
(
k
)
:
ω
4
−
ω
2
ω
2
l
+
ω
2
la
+
ω
2
l
ω
2
la
+
c
2
0
k
2
−
c
2
0
k
2
ω
2
0
a
+
c
2
0
k
2
= 0
.
(7)
Решения уравнения (7) имеют вид
ω
2
±
=
ω
2
l
+
ω
2
la
2
1
±
s
1
−
4 [
ω
2
l
(
ω
2
la
+
c
2
0
k
2
)
−
c
2
0
k
2
(
ω
2
0
a
+
c
2
0
k
2
)]
(
ω
2
l
+
ω
2
la
)
2
!
.
(8)
Для определенности выберем следующие значения параметров,
см
−
1
:
ν
0
a
= 2
;
ν
1
a
= 1
;
ν
1
= 5
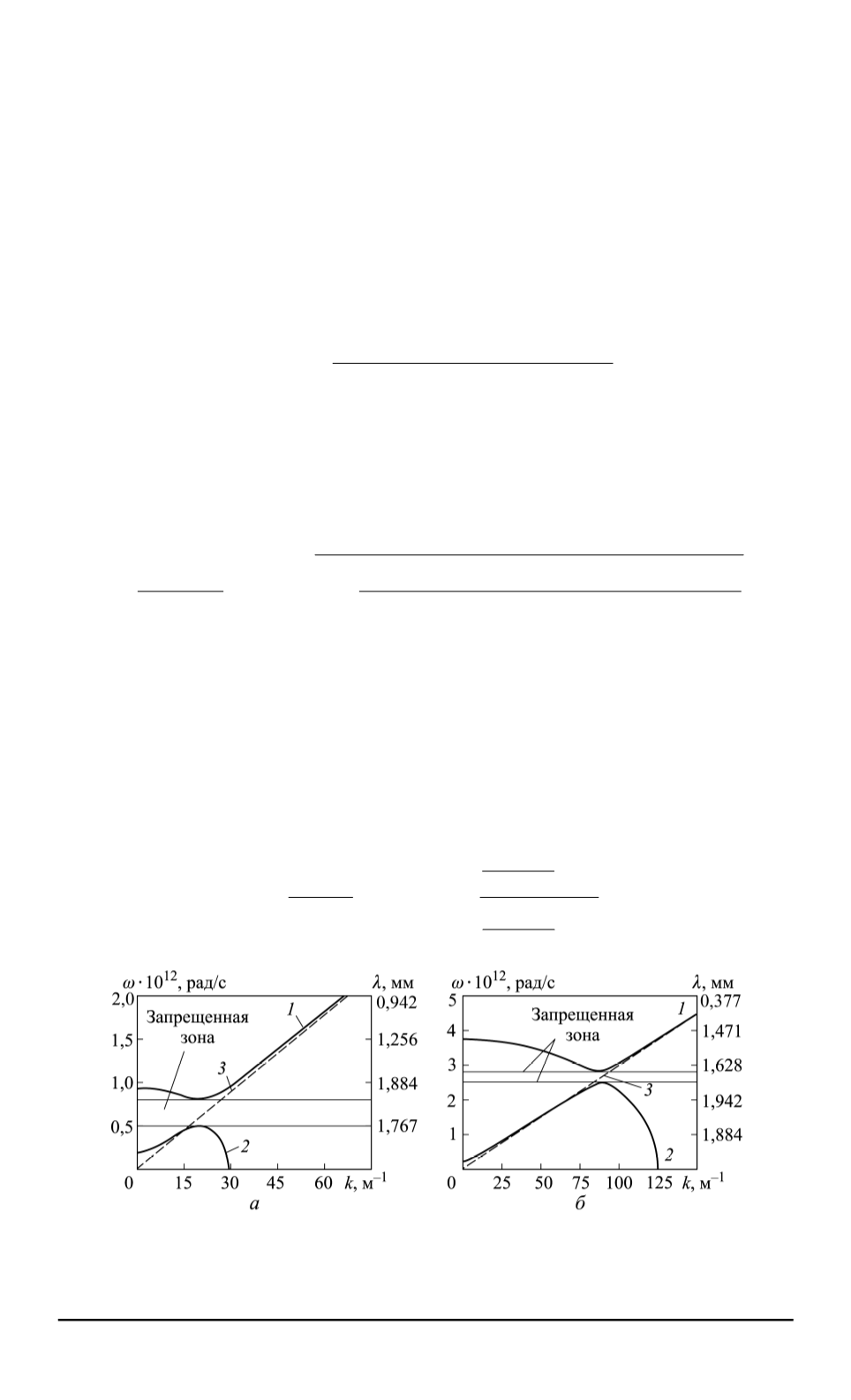
. Для указанных значений соответствую-
щие дисперсионные зависимости, построенные с помощью уравнения
(8), представлены на рис. 1,
а
.
Групповую скорость, коэффициент отражения и показатель пре-
ломления можно вычислить с помощью следующих формул:
V
gr
=
dω
(
k
)
dk
;
R
(
ω
) =
c
0
k
(
ω
)
ω
−
1
c
0
k
(
ω
)
ω
+ 1
2
;
Рис. 1. Дисперсионные зависимости
ω
(
k
)
для метаматериала в магнитном поле
при
ν
l
= 5
см
−
1
(
а
) и
ν
l
= 20
см
−
1
(
б
):
1
,
2
— кривые для
ω
2
+
,
ω
2
−
(8);
3
— закон дисперсии фотонов в вакууме
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 1
39
















