
В.И. Вишняков, С.М. Вишнякова, П.В. Дружинин
18
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
направление, перпендикулярное движению жидкости;
η
— коэффициент ди-
намической вязкости. Жидкости, описываемые законом (1), называются бинга-
мовскими, или вязкопластическими. Эта модель успешно применяется как в
классической, так и в магнитной гидродинамике [6–8]. При течении таких
жидкостей в каналах возможно образование двух зон течения: 1) зоны вязкого
течения, когда
0
;
τ > τ
2) зоны пластического течения, когда
0
.
τ < τ
Общая картина течения получается из решений уравнений движения
жидкости в указанных зонах с учетом соответствующих условий на границе
раздела зон [6], что позволяет рассматривать движение в каждой зоне отдельно.
Далее рассмотрена задача о влиянии скачкообразного изменения внешнего
магнитного поля на ширину зоны пластического течения в бесконечном плос-
ком канале. Необходимость решения подобной задачи связана с тем, что при
резком возрастании магнитного поля зона пластического течения может запол-
нить большую часть канала (или весь канал), создав тем самым пробку.
Постановка задачи о движении магнитопроводящей жидкости в плоском
канале аналогична постановке известной задачи Гартмана [9].
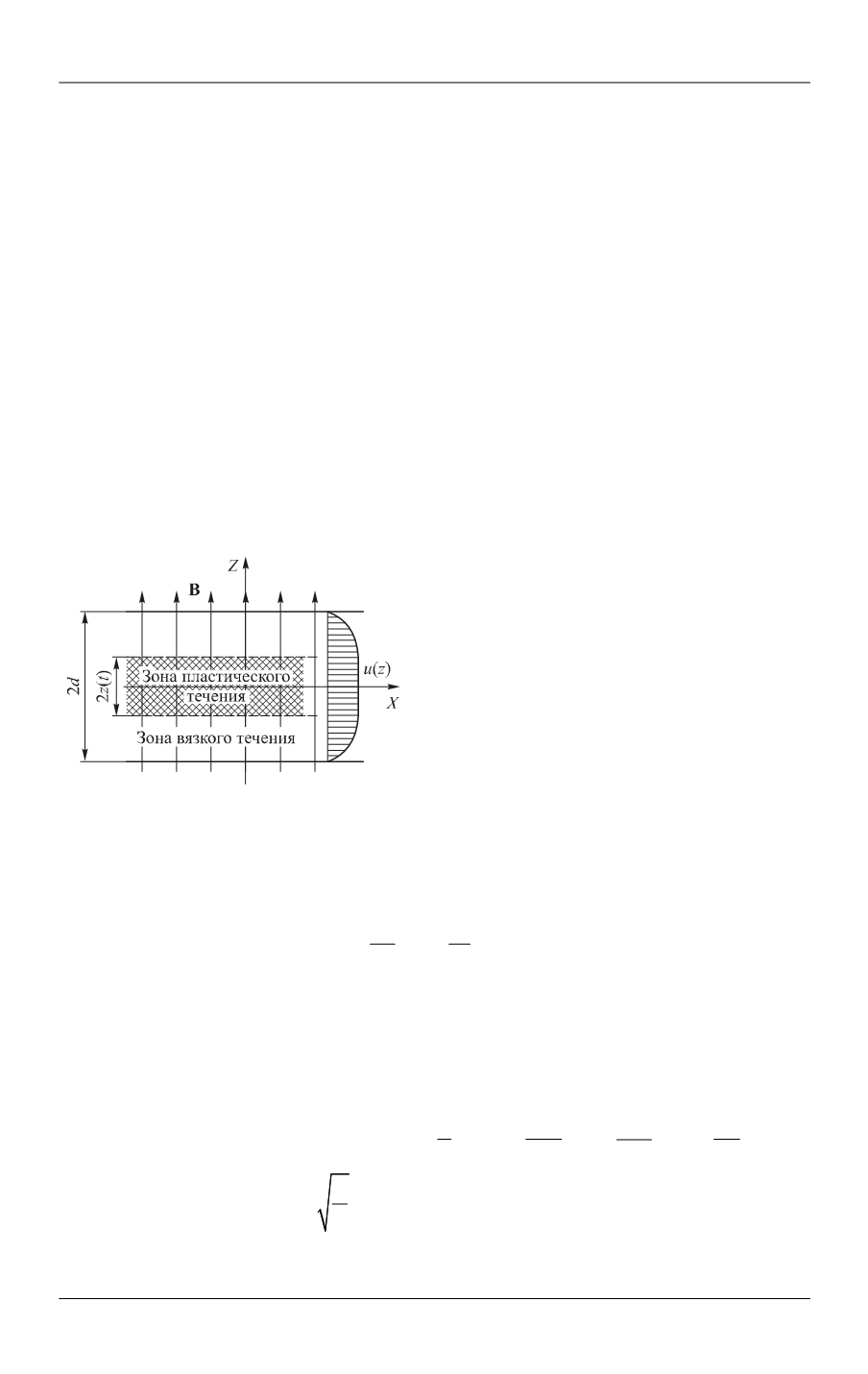
Схема течения жидкости приведена
на рис. 1, где направление течения совпа-
дает с осью
,
X
координата
z
отсчитыва-
ется от середины канала шириной
2 .
d
Граница, положение которой задается
функцией
( ),
z t
разделяет зону вязкого
течения и зону пластического течения.
Вектор индукции внешнего магнитного
поля
B
направлен вдоль оси
.
Z
Нестационарное уравнение движе-
ния, записанное ранее для зоны пласти-
ческого течения [8], в таком случае имеет
вид
0
2
.
du P
B u
dt
z
τ
ρ = − −σ
(2)
Здесь
( )
z z t
=
— уравнение границы раздела зон;
ρ
— плотность жидкости,
предполагаемая постоянной;
( )
u u t
=
— скорость жидкости в канале;
P
— по-
стоянный градиент давления;
σ
— проводимость жидкости.
Приняв в качестве характерных параметров безразмерные комбинации ранее
рассмотренных физических величин
,
z z
d
=
2
,
V u
Pd
η =
2
,
t
t
d
η=
ρ
0
S
Pd
τ=
(пара-
метр Сен-Венана),
H Bd
σ =
η
(критерий Гартмана), запишем уравнение (2)
в безразмерной форме:
Рис. 1.
Схема течения магнитопрово-
дящей жидкости в плоском канале при
наличии поперечного магнитного поля
















