
С.В. Федоров
74
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
Упорядоченного Движения Индивидуальных Точек), реализующая вычислитель-
ный алгоритм, который основан на методе свободных лагранжевых точек [15].
Достаточно подробно этот алгоритм описан в работах [16, 17], алгоритм был
апробирован на численном решении широкого круга задач взрывного и ударного
нагружения сплошных сред и хорошо себя зарекомендовал [18–20]. К числу его
достоинств следует отнести возможность расчета движений сплошной среды с
большими деформациями без использования специальных процедур перестрой-
ки расчетной сетки.
В расчетах рассмотрен цилиндрический кумулятивный заряд диаметром
d
0
= 100 мм и высотой
h
0
= 150 мм с облицовками различной формы из меди
(рис. 1). Параметры кумулятивных струй из полусферических облицовок срав-
нивались с параметрами струи, формируемой конической облицовкой прогрес-
сивной толщины (увеличивающейся от 1,4 мм в вершине до 2,6 мм у основания)
с углом раствора 60
°
и внутренним диаметром основания 90 мм (рис. 1,
а
). Зада-
вавшиеся геометрические параметры конической облицовки (в соотношении с
рассматриваемым диаметром заряда) являются типичными для современных
кумулятивных зарядов с линзовым узлом, обладающих максимальным (в соот-
ношении с диаметром) пробивным действием [2].
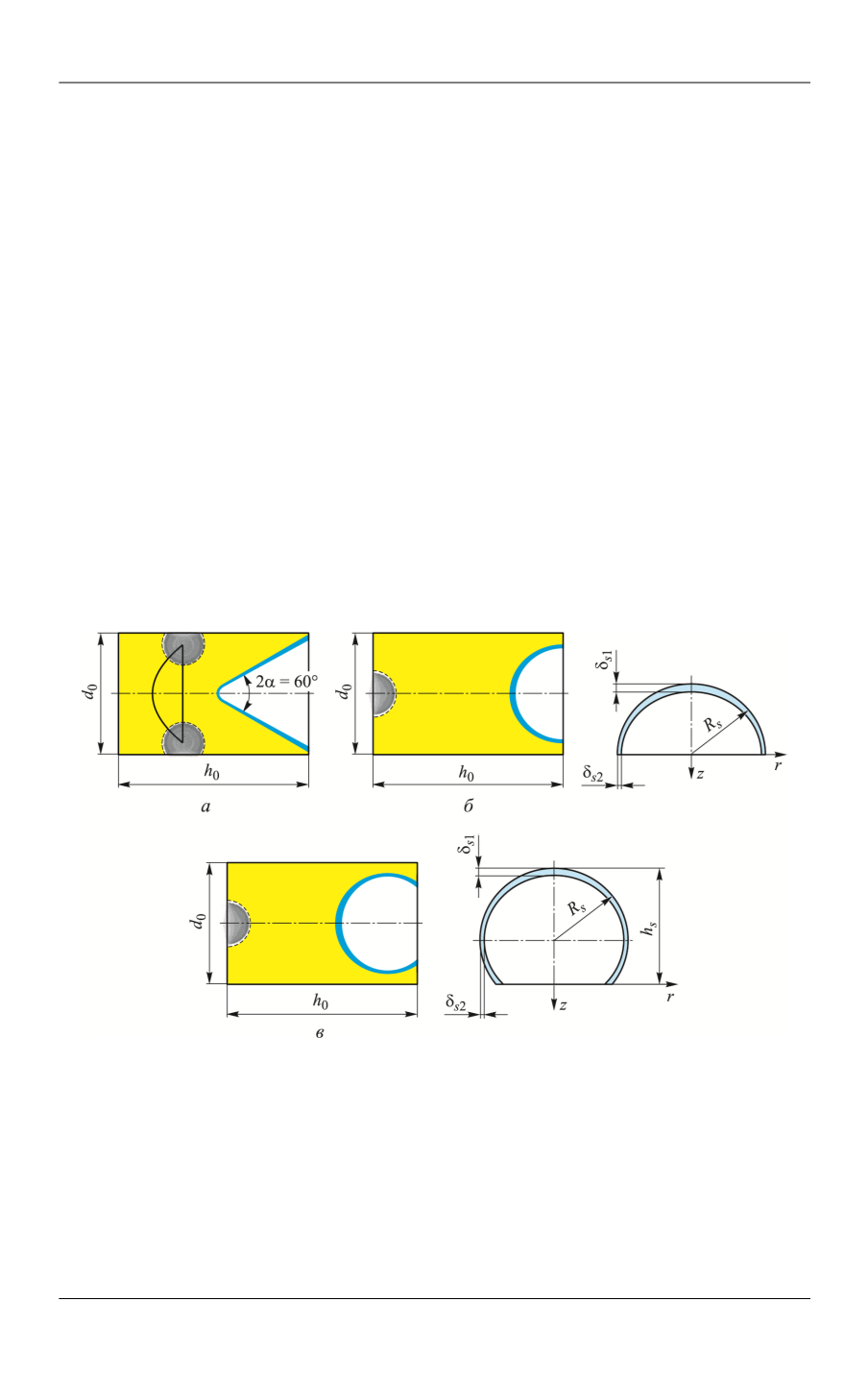
Рис. 1.
Схемы кумулятивных зарядов с конической облицовкой и линзовым узлом (
а
), с
полусферической облицовкой (
б
) и с облицовкой в форме усеченной сферы (
в
)
Наружный радиус рассматриваемых полусферических облицовок составлял
R
s
= 40 мм, их толщина при вершине δ
s
1
= 2,4 мм, а толщина у основания δ
s
2
ва-
рьировалась в диапазоне 2,4…1,0 мм (рис. 1,
б
). Дегрессивность толщины полу-
сферических облицовок обеспечивалась тем, что при полусферической форме
внешней поверхности их внутренняя поверхность задавалась в форме слегка
















